আমার লেখার হাত অতটা ভালো না। তাই খুব একটা লিখি না। তবে এই বিষয়টা নিয়ে একটু লেখতে ইচ্ছা করল তাই শুরু করলাম। ঘটনার সুত্রপাত আমি যখন ইন্টারে উঠলাম তখন। আমাদের বইতে দ্বিপদী উপপাদ্য নামে একটা জিনিস(!!) পড়ানো হয় (কিংবা গলধকরন করানো হয়)। আগে সবাইকে মনে করিয়ে সেটা দেই।
$$(a+b)^n=^{n}\textrm{C}_{0} a^n +^{n}\textrm{C}_{1}a^{n-1}b+\cdots \cdots+^{n}\textrm{C}_{r} a^n b^{n-r}+\cdots \cdots+^{n}\textrm{C}_{n}b^n$$
আচ্ছা মোটামুটি সবাই এটা জানে। কিন্তু এইখানে $^{n}\textrm{C}_{r}$ আকারের পদগুলো যে কারও ইচ্ছা অনুযায়ী আসে নি বরং এর পেছনে যে কিছু চমৎকার কারন আছে সেটা অনেকেই জানে না। আর অতি দুর্ভাগ্যর বিষয় আমাদের পাঠ্য বইতে এইসমস্ত বিষয় কখনই পড়ানো হয় না।
এবার আসুন একটু আবার বিন্যাস-সমাবেশ মনে করিয়ে দিই। এই সমস্যাটা মুলত গনিতের যে শাখায় আলোচিত হয় তার নাম Combinatorics (এর সঠিক বাংলা পরিভাষা জানি না। তবে সত্যন বোস একবার এর বাংলা হিসাবে “মহাসমারোহ তত্ত্ব” ব্যবহার করেছিলেন)
আচ্ছা, এখন বলুনতো $aabbbb$ এটাকে ঠিক কতভাবে বিন্যাস করা যায়। উত্তর অনেকেই জানেন $\frac{6!}{2!4!}$ ভাবে। (কেন এমন হল সেদিকে আর আজকে গেলাম না, সে এক আরেক ইতিহাস) আচ্ছা আরেকটা ফর্মুলা মনে করিয়ে দেই,
$$^{n}\textrm{C}_{r}=\frac{n!}{r!(n-r)!}$$
$^{n}\textrm{C}_{r}$ মানে হল $n$ সংখ্যক বস্তু হতে $r$ সংখ্যক বস্তু কতভাবে বেছে নেয়া যায়। আপাতত এইটুকু জানলেই আমাদের চলবে।
এবার আসি আসল কথায়। ধরুন $(a+b)^3$ কে বিস্তৃত করতে হবে। তাহলে, আমরা যেটা করতে পারি সেটা হল $(a+b)(a+b)(a+b)$ এই গুনটা করবো এখন সেই বাচ্চাকালের নিয়মে আগানো যাক। প্রথমে $b$ দিয়ে গুন শুরু করি। তাহলে পদগুলো দাঁড়ায়, $b\cdot b\cdot b+b\cdot b\cdot a+b\cdot a \cdot b+b\cdot a \cdot a$ আবার $a$ দিয়ে গুন করলে পদ্গুলো হয়, $a\cdot b\cdot b+a\cdot b\cdot a+a\cdot a\cdot b+a\cdot a\cdot a$ এখন বেশ মজার একটা জিনিস দেখি, $b\cdot b\cdot a$ এই জিনিসটা এসেছে ৩ বার। মজার ব্যাপার হল এটাকে আসলে ৩ ভাবেই সাজানো যায়। $\frac{3!}{2!} = 3$ আবার $a\cdot a\cdot b$ কেউ ৩ ভাবে সাজানো যায়। তাহলে আসলে আমরা এখানে কী করেছি যে এমন হল? আসলে বিষয়টা অনেক সোজা। আমরা এখানে যখন $a,b$ দিয়ে ধারাবাহিকভাবে গুন করছিলাম তখনি আমরা সাজানোর কাজটা করে ফেলেছি। আপনারা চাইলে $(a+b)^4,(a+b)^6$ ইত্যাদি গুলা নিজেরা করে দেখতে পারেন। এবার আরও বড় কিছু করি। $(a+b)^{11}$ এর জন্য $b\cdot b\cdot b\cdot b\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a$ পদটার সহগ কিভাবে বের করা যায়। আমরা ফরমুলাটা জানি। কিন্তু আমরা একটু আগেই বিন্যাস দিয়ে করা শিখেছি তাই আমরা বিন্যাস দিয়ে করবো। তাহলে সহগ হবে, $\frac{11!}{4!6!} = 330$ আবার ফর্মুলাতেও কিন্তু $330$ আসে।
$$^{11}\textrm{C}_{4}=\frac{11!}{4!(11-6)!}=330$$
অনেকেই নিশ্চয়ই বুঝে ফেলেছেন এখন ফর্মুলাটা কিভাবে আসলো। তবুও আমি দেখিয়ে দিচ্ছি। মনেকরি, $(a+b)^n$ কে বিস্তৃত করতে হবে। তাহলে আমার কাছে প্রতি পদে $a$ এবং $b$ দুটো মিলিয়ে আমার কাছে মোট $n$ সংখ্যক জিনিস থাকে এবং তাদেরকে আমরা যতভাবে সাজাতে পারি তার সংখ্যাই হবে তার সহগ। এখন মনে করি একটি পদে $r$ সংখ্যক $b$ আছে এবং তাহলে অবশ্যই $(n-r)$ সংখ্যক $a$ থাকবে। তাহলে তাদের সাজানো যাবে মোট, $\frac{n!}{r!(n-r)!}$ ভাবে। কিন্তু মজার ব্যাপার হল,
$$^{n}\textrm{C}_{r}=\frac{n!}{r!(n-r)!}$$
ব্যাস, আমাদের কাজ শেষ। এখন সবাই জানেন কিভাবে এই সহগ গুলা আসে। আমার কাছে অনেক দুঃখ লেগেছে এই দেখে যে আমাদের দেশের অনেক শিক্ষকও এই বিষয়টি জানেন না। আর আমাদের বইতে এই চমৎকার প্রমাণটি বাদ দিয়ে অনেকটা দুর্বোধ্য গানিতিক আরোহ পদ্ধতি পড়ানো হয়। গানিতিক আরোহ পদ্ধতি পড়ানো নিয়ে আমার কোনো সমস্যা নাই কিন্তু কেন আমাদের শিক্ষার্থীরা গনিতের এই সৌন্দর্য থেকে বঞ্চিত হবে। সব শেষে আমি কিছু সমস্যা দেয়ার লোভ সামলাইতে পারলাম না। গনিতের সবচেয়ে মজার অংশ হল সমস্যা সমাধান করা। আমি কিছু চমৎকার সমস্যা দিচ্ছি, আশা করি আপনারা চেষ্টা করবেন।
সমস্যাঃ
১. যারা প্যাস্কেলের ত্রিভুজ চেনেন তারা প্যাস্কেলের ত্রিভুজের একটি row এর সবগুলো সংখ্যার যোগফল বের করেন।
২. $0$ থেকে $9$ পর্যন্ত সকল সংখ্যা ব্যবহার করে ৬ অঙ্কের যতগুলো সংখ্যা তৈরি করা সম্ভব তাদের সকলের যোগফল বের কর।উল্লেখ্য একই অঙ্কের পুনরাবৃত্তি করা যাবে না অর্থাৎ একটা অঙ্ক মাত্র একবার ব্যাবহার করা যাবে। (মিলন ভাইয়ের দেয়া সমস্যা)
৩. ২ নং এর সমস্যাটায় $n$ অঙ্কের সকল সংখ্যার যোগফল কত হবে ? (Generalization)
৪. ৩নং সমস্যাটিতে পুনরাবৃত্তি গ্রহণযোগ্য হলে যোগফল কত হবে ?
৫. $(a+b)^{2010}$ এর বিস্তৃতিতে বিজোড় সহগবিশিষ্ট পদের সংখ্যা কতগুলো? (Bangladesh Mathemtical Olympiad-2010) [Problem Setter: অভিক রায়]
তথ্য সুত্রঃ
১. Notes on combinatorics by Tarik Adnan Moon (Bronze Medalist from Bangladesh)
২. Wikipedia articles
৩. Principles and Techniques in Combinatorics by Chen Chuan-Chong and Koh Khee-Meng, National University of Singapore.
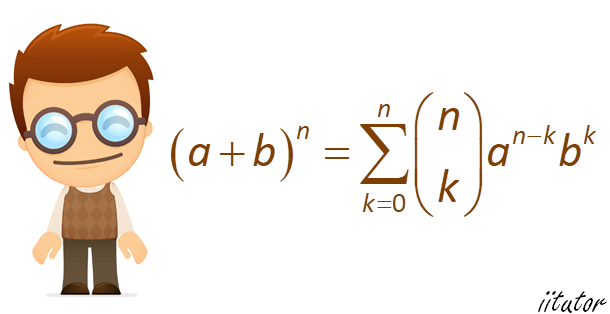
Leave a Reply