প্রথমেই বলে রাখি লেখাটি বিশেষ করে স্কুল-কলেজ পড়ুয়া পাঠকদের জন্য যাদের পদার্থবিজ্ঞানে একটু হলেও আগ্রহ আছে। যারা বিশেষ আপেক্ষিকতা একটু-আধটু জানে-বোঝে, তারা সবাই আশা করি দৈর্ঘ্যের আপেক্ষিকতা বা দৈর্ঘ্য-সংকোচন বিষয়টি জানে। বইয়ের ভাষায়ঃ
কোন পর্যবেক্ষকের সাপেক্ষে গতিশীল বস্তুর দৈর্ঘ্য ঐ পর্যবেক্ষকের সাপেক্ষে নিশ্চল অবস্থায় ঐ একই বস্তুর দৈর্ঘ্যের চেয়ে ছোট হয়, এই প্রভাবকে দৈর্ঘ্য সংকোচন বলে।

সহজ কথায়, কোন বস্তু যদি আপনার তুলনায় অতি উচ্চ বেগে গতিশীল থাকে, তবে বস্তুটির দৈর্ঘ্য তার গতির অভিমুখ বরাবর আপনার সাপেক্ষে সংকোচিত হয়ে যায়। আবার এর বিপরীত ঘটনাও সত্য। বস্তুটির সাপেক্ষে সম্পূর্ণ জগত তার গতির অভিমুখ বরাবর সংকোচিত হয়ে যায়।
এ লেখায় আমি এই দৈর্ঘ্য-সংকোচনেরই একটি খুব সাধারণ কিন্তু চমৎকার দিক আলোচনা করব।
এখানে, আমি যে বিষয়টিতে দৃষ্টি আকর্ষণ করাতে চাচ্ছি, সেটা হল গতির অভিমুখ। যারা স্কুল-কলেজ পর্যায়ে দৈর্ঘ্য-সংকোচন পড়েছেন, খেয়াল করবেন দৈর্ঘ্যের উপর আপেক্ষিকতার প্রভাব সহজ হিসাবে কেবল গতির অভিমুখ বরাবর বিবেচনায় আনা হয়। কিন্তু তার মানে কি এই নয় যে আপেক্ষিকতার প্রভাব শুধু গতির অভিমুখ বরাবরই থাকে?

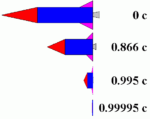
এর উত্তরে আসার আগে এ লেখার বিষয়বস্তু স্পষ্ট বোঝানোর জন্য একটা উদাহরণ দেই – আপনার বন্ধু অতি উন্নত একটা রকেটে (উপরের ছবিতে) অবস্থান করছেন। আপনি পৃথিবী থেকে সর্বক্ষণ রকেটটি পর্যবেক্ষন করছেন। আপনার বন্ধু রকেটের বেগ অতি উচ্চ হারে বাড়াতে শুরু করলে রকেটের নীল আয়তাকার প্রপালশন সিস্টেমের দৈর্ঘ্য-সংকোচন খুব স্বাভাবিক ভাবেই আপনার চোখে পড়ে। কিন্তু আপনি একটু মনোযোগ দিলে খেয়াল করে দেখলেন, প্রাথমিক অবস্থায় রকেটের সামনের লাল নোজকোন (পেলোড সিস্টেম) এবং পেছনের গোলাপী ফিন দুটি ত্রিভুজ আকৃতির ছিল, নোজকোনটি প্রায় সমদ্বিবাহু আর ফিন দুটি সমকোণী ত্রিভুজ। আপনি আরো খেয়াল করলেন, গতিবেগ বৃদ্ধির সাথে সাথে লাল নোজকোনের তিনটি কোণেই দৈর্ঘ্য-সংকোচনের প্রভাব লক্ষণীয়, কিন্তু ফিন দুটির সমকোণটির উপর আপেক্ষিকতার কোন প্রভাব নেই। তাহলে কেন এমনটা হচ্ছে? আবার এ ত্রিভুজ তিনটির প্রতিটি বাহুর; কি দৈর্ঘ্য-আপেক্ষিকতার প্রভাব একই হবে? বাহুগুলোর দৈর্ঘ্য-সংকোচন কি একই ভাবে হিসাব করা যাবে? আবার প্রাথমিক বা স্থির অবস্থায় (বেগ $0c$) কোণগুলোর মান এবং গতিশীল অবস্থায় কোনগুলোর মান ভিন্ন, তাহলে এদের এদের মধ্যকার সম্পর্ক কেমন? গতিশীল অবস্থার কোণের মান কিভাবে আমরা নির্ণয় করব?
একটা উদাহরণ দিতে গিয়ে বেশ কিছু প্রশ্ন করে ফেললাম। আসলে এই প্রশ্নগুলোই উত্তরই আজ আলোচনার বিষয়। তাই চলুন দেরি না করে গাণিতিক ভাবে বিষয়টা চিন্তা করা যাক।
প্রথমেই ধরে নিই,
স্থির কাঠামো থেকে দেখা যায়,
একটা সরলরেখার দৈর্ঘ্য $AC=L_o$, এটা $AB$ পথের সাথে $\theta_o$কোণে আনত। অর্থাৎ, $∠BAC=\theta_o$। এখানে ${BC}\perp{AB}$ আঁকি।
আবার, $AB$ পথ বরাবর বেগ $v$ (আলোর বেগ $c$ এর খুব কাছাকাছি) বিশিষ্ট গতিশীল কাঠামো থেকে দেখা যায়,
সরলরেখাটির দৈর্ঘ্য $A’C’=L$, যা $AB$ পথের সাথে $\theta$ কোণে আনত। অর্থাৎ, $∠B’A’C’=\theta$। এখানে ${B’C’}\perp{A’B’}$ আঁকি।
আমরা দেখেছি গতিপথের লম্ব বরাবর রেখার উপর দৈর্ঘ্য-সংকোচনের প্রভাব নেই। আপাতত এটার কারণ না জানলেও (আশা করি কিছুক্ষণের মধ্যে জানতে পারব) বলা যেতে পারে $C$ বিন্দুর ( গতিশীল কাঠামোতে যা $C’$ দ্বারা চিহ্নিত) উচ্চতা উভয় কাঠামো থেকেই সমান হয়। অর্থাৎ ${BC}\parallel{B’C’}$ হওয়ার পাশাপাশি বলতে পারি, $BC=B’C’$।
[ বিঃদ্রঃ পাঠকদের মধ্যে যারা তুখোড় গণিতবিদ তাদের উদ্দেশ্যে বলছি, আপনারা হয়তো ভুরু কুচকে জিজ্ঞেস করতে চাইবেন- “লম্ব রেখার উপর দৈর্ঘ্য-সংকোচনের প্রভাব নেই” প্রমাণ করার আগেই সেটা প্রতিপাদনের মধ্যে ব্যবহার করা কতটা যুক্তি-সঙ্গত? আসলে কোণ আপেক্ষিকতার এই সম্পূর্ণ ব্যাপারটা লরেঞ্জ রূপান্তর-এর মাধ্যমে মৌলিক ভাবে প্রমাণ করা যেত। কিন্তু সব বয়সী আগ্রহী পাঠকদের কথা চিন্তা করে আমি সহজে ব্যাপারটি বোঝানোর জন্য প্রমাণের আগেই $BC=B’C’$ ব্যবহার করলাম। আশা করি বিষয়টা আপনারা ক্ষমা-সুন্দর দৃষ্টিতে দেখবেন। ]
এখন এইদুটি ভিন্ন কাঠামো থেকে দেখা দুটি ভিন্ন দৃশ্যায়নকে যদি একসাথে সমন্বয় করি, তার ছবিটি হবে নিম্নরূপঃ

সাধারণ ত্রিকোণমিতি ব্যবহার করে বলা যায়,
$AB=L_o\cos{\theta_o}$ এবং $BC=B’C’=L_o\sin{\theta_o}$।
আবার গতিশীল কাঠামোর বেগ $AB$ পথ বরাবর থাকায় দৈর্ঘ্য সংকোচনের নীতি অনুসারে লেখা যায়,
$A’B’=\frac{AB}{\gamma}=\frac{L_o\cos{\theta_o}}{\gamma}$ যেখানে লরেঞ্জ সহগ, $\gamma=\frac{1}{\sqrt{1-(v/c)^2}} $
এখন $∆A’B’C’$ এ পিথাগোরাসের উপপাদ্য ব্যবহার করে পাওয়া যায়,
$$ \begin{align} (A’C’)^2 &= (A’B’)^2+(B’C’)^2 \\ \implies L^2 &= \left(L_o\frac{\cos{\theta_o}}{\gamma}\right)^2 +(L_o\sin{\theta_o})^2 \end{align} $$
$$\therefore \, L=L_o\sqrt{1-\left(\frac{v \cos{\theta_o}}{c}\right)^2} \quad ∎$$
তাহলে এটাই সেই সমীকরণ যা পর্যবেক্ষকের গতিপথের সাথে যেকোনো কোণে আনত দৈর্ঘ্যের উপর আপেক্ষিকতার প্রভাব ব্যাখা করে। লক্ষ করুন সমীকরণে আপেক্ষিক বেগের সাথে আছে কোণের কোসাইন। অর্থাৎ যখন সরলরেখার দৈর্ঘ্য গতিবেগের অভিমুখ বরাবর থাকে $(\theta_o=0^\circ,\,\cos{\theta_o}=1)$, তখন তা দৈর্ঘ্য সংকোচনের সাধারণ সমীকরণকেই প্রকাশ করে, তখন $L=L_o\sqrt{1-(v/c)^2}=L_o/\gamma$ হয়। কিন্তু সরল রেখাটি যদি গতিবেগের লম্ব বরাবর থাকে $(\theta_o=90^\circ,\,\cos{\theta_o}=0)$, তখন $L=L_o$ হয়। অর্থাৎ গতিপথের সাথে লম্বভাবে স্থাপিত সরলরেখার দৈর্ঘ্যের উপর আপেক্ষিকতার প্রভাব থাকে না।
কলেজ পড়ুয়া পাঠকেরা খেয়াল করবেন এ ব্যাপারটিকে ভেক্টর ব্যবহার করে আরো সহজে ব্যাখা করা যায়। যেহেতু বেগ $(\vec{v})$ একটি ভেক্টর রাশি, তাই $L_o$ দৈর্ঘ্যের সরল রেখা $\vec{v}$ এর ক্রিয়ারেখার সাথে $\theta_o$ কোণে আনত থাকায় $L_o$ বরাবর $\vec{v}$ এর উপাংশ থাকে $v \cos{\theta_o}$। তাই $L_o$ এর আপেক্ষিকতার প্রভাব সম্পূর্ণ $v$ দ্বারা না হয়ে শুধু $v\cos{\theta_o}$ দ্বারা নিয়ন্ত্রিত হয়। তাই মূল সমীকরণে $v$ এর বদলে $v\cos{\theta_o}$ ব্যবহার করলেই হয়।
এবার চলুন ছবিটির দিকে আবার তাকাই। এখন প্রকৃত কোণ $\theta_o$ এবং আপেক্ষিক কোণ $\theta$ এর সম্পর্ক কেমন হয় সেটা দেখা যাক।

চিত্র অনুসারে প্রকৃতকোণ (স্থির কাঠামোতে দেখা কোণ), $∠BAC=\theta_o$
আপেক্ষিক কোণ (গতিশীল কাঠামোতে দেখা কোণ), $∠B’A’C’=\theta$
এখন $∆A’B’C’$ থেকে পাই,
$$\begin{align} \tan{\theta} &= \frac{B’C’}{A’B’} \\ \implies \tan{\theta} &= \gamma \frac{L_o \sin{\theta_o}}{L_o \cos{\theta_o}} \\ \implies \tan{\theta} &= \gamma\tan{\theta_o} \end{align}$$
$\therefore \, \tan{\theta}=\frac{\tan{\theta_o}}{\sqrt{1-(\frac{v}{c})^2}} \quad ∎ $
এটাই হল কোণ-আপেক্ষিকতার সমীকরণ।
সমীকরণটির দিকে তাকালে এর একটা চমৎকার দিক দৃষ্টিগোচর হয়। সমীকরণটিতে আছে কোণের ত্রিকোণমিতির tangent ফাংশন। যা আমাদের প্রকাশ করে বিশেষ আপেক্ষিকতায় আপেক্ষিক কোণ ও প্রকৃত কোণের মধ্যকার সম্পর্ক সবসময় একই রকম হবে না (ভর, দৈর্ঘ্য বা কালের আপেক্ষিকতায় বেলায় এমনটা হয় না)। কখনো আপেক্ষিক কোণ প্রকৃত কোণ থেকে ছোট, কখনো বড়, আবার কখনো সমান হবে। এ শর্ত নির্ভর করে কোণের মানের উপর।
এ শর্তগুলো গাণিতিকভাবে প্রকাশ করলে হবে এমন,
- যখন $\theta_o=0^\circ$ অথবা $\theta_o=90^\circ$, তখন $\theta=\theta_o$ [কোণ অপরিবর্তন]
- যখন $0^\circ<\theta<90^\circ$, তখন $\theta>\theta_o$ [কোণ সম্প্রসারণ]
- যখন $\theta>90^\circ$, তখন $\theta<\theta_o$ [কোণ সংকোচন]
অর্থাৎ, প্রকৃত কোণ যদি $0^\circ$ বা $90^\circ$ হয় তখন কোণের উপর আপেক্ষিকতার প্রভাব থাকে না। তাই প্রকৃত কোণ ও আপেক্ষিক কোণ পরস্পর সমান হয়। কিন্তু প্রকৃতকোণ যদি $0^\circ$ থেকে বড় কিন্তু $90^\circ$ থেকে ছোট হয়, তখন কোণ সম্প্রসারণ হয় (কাল দীর্ঘায়নের মত)। আবার প্রকৃত কোণ যখন $90^\circ$ থেকে বড় হয় তখন বিপরীত ঘটনা ঘটে, কোণ সংকোচন ঘটে। সেই সাথে আরেকটা তাৎপর্যপূর্ণ ব্যাপার এই সমীকরণটি প্রকাশ করে তা হল যদি প্রকৃত কোণ $\theta_o≠90^\circ$ হয় তবে কখনোই আপেক্ষিক কোণ $\theta=90^\circ$ হবে না, যতক্ষণ না বেগ আলোর বেগের সমান হয়। কারণ, $\theta=90^\circ$ হওয়ার অর্থ বেগের অভিমুখ বরাবর দৈর্ঘ্যের উপাংশ শূন্য হওয়া এবং দৈর্ঘ্যের আপেক্ষিকতা থেকে আমরা জানি এটা কেবলমাত্র আলোর বেগে চললেই সম্ভব।
ব্যাপারটি অদ্ভুত রকম চমৎকার, তাই না?
চিন্তা করে যদি মজা পেয়ে থাকেন, তবে পাঠকদের বলব এ সম্পর্কিত নিচের সমস্যাটি সমাধান করুন –
সমস্যাঃ
একজন কৃষক একটা চারকোণা সমতল মাঠের প্রতি বর্গমিটারে $10$ টি চারাগাছ লাগাতে চান। তিনি তার বিশেষ গাড়িতে চড়ে মাঠের একটি ধার বরাবর ভ্রমণ করতে করতে বিশেষ যন্ত্র দিয়ে হিসাব করলেন মাঠটি রম্বস আকৃতির, যার ক্ষেত্রফল $20$ বর্গ কি.মি.। গাড়ি থামিয়ে মাঠে নেমে দেখলেন মাঠের দুটি ধারের মধ্যবর্তী কোণ $60^\circ$। সেই হিসেবে তিনি চারা সংগ্রহ করলেন। কিন্তু চারা লাগানোর সময় দেখলেন তাঁর আরো চারা প্রয়োজন। তাহলে এই কৃষকের অতিরিক্ত কতটি চারা প্রয়োজন এবং কেন? (যে কথাটা বলা হয়নি, আশ্চর্যজনকভাবে তাঁর বিশেষ গাড়িটি $0.8c$ সমবেগে চলে!)
Leave a Reply