বিজ্ঞান বিনোদন
%22%20transform%3D%22translate(3.7%203.7)%20scale(7.34375)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23d06816%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(-12.4%20534.2%20-765.5)%20scale(32.77421%2041.22533)%22%2F%3E%3Cellipse%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(8.00974%20-254.87417%2082.27454%202.58558%2043.2%2083.4)%22%2F%3E%3Cpath%20fill%3D%22%23313424%22%20d%3D%22M209%2038l-68-28-25%2093z%22%2F%3E%3Cellipse%20fill%3D%22%23a66b3d%22%20cx%3D%22178%22%20cy%3D%2299%22%20rx%3D%2217%22%20ry%3D%2217%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
পানিতে জ্বলবে আলো
দরিদ্র মানুষের চাল নেই, চুলোও নেই। ঘরে বিদ্যুৎবাতি তো দূরের কথা, এই আকালের দিনে দুফোঁটা কেরোসিনেরও খোঁজ পাওয়া যায় না, তাই ঘুটঘুটে অন্ধকারে চাঁদের আলোই ভরসা। কিন্তু সুদূর ফিলিপাইনের দুই ভাইবোনের তৈরি এক বাতি চলবে লবণপানিতে। এতে স্বস্তির নিশ্বাস ফেলতে পারবেন অনেকেই। আইসা এবং রাফায়েল মিজেনো নামের এই দুই সহোদর sALt (Sustainable Alternative Lighting) নামের…
%22%20transform%3D%22translate(.5%20.5)%20scale(1.03516)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23dba100%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(28.24705%2038.31337%20-47.59955%2035.09342%2083.8%20144)%22%2F%3E%3Cellipse%20fill%3D%22%23a2dbff%22%20cx%3D%22169%22%20cy%3D%22255%22%20rx%3D%2271%22%20ry%3D%2276%22%2F%3E%3Cellipse%20fill%3D%22%239a5986%22%20cx%3D%2299%22%20cy%3D%22193%22%20rx%3D%2240%22%20ry%3D%2231%22%2F%3E%3Cellipse%20fill%3D%22%2397e7ff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(3.50025%20176.96539%20-20.86841%20.41276%20166.6%20104.3)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
গণিতর সৌন্দর্য- পর্ব ২৩: অভিপ্রেতানভিপ্রেত কাকতাল
কাকতাল বলতে কী বোঝায় আর কাকতালে কেনই আমরা বিস্ময়াভীভূত হই? অভিধান ঘেঁটে কাকতাল অর্থ পাওয়া গেল এমন: “কার্যকারণ সম্বন্ধ নাই অথচ একসঙ্গে সঙ্ঘটিত দেখিয়া মনে হয় পরস্পর সম্বন্ধযুক্ত”। এবার বিষয়টি একটু ব্যখ্যা করা যাক। ধরা যাক আপনার সাথে আপনার অফিসের বসের বেশ রাগারাগি হলো। আপনি তাঁর প্রতি বেশ অসন্তুষ্ট হওয়ায় বাসায় ফিরে ঠান্ডামাথায় সেটি নিয়ে…
%22%20transform%3D%22translate(.5%20.5)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23d3d3d3%22%20cx%3D%2254%22%20cy%3D%2272%22%20rx%3D%22107%22%20ry%3D%2217%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20cx%3D%22108%22%20cy%3D%2211%22%20rx%3D%22146%22%20ry%3D%2229%22%2F%3E%3Cpath%20fill%3D%22%23d1d1d1%22%20d%3D%22M108%2017l29%2042-47-2z%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(22.12213%20.671%20-1.14814%2037.85252%2072.7%2027.2)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
অনুমান ও কোয়ান্টাম বিক্ষিপ্ততা (অণুপোস্ট)
‘অনুমান’ বৈজ্ঞানিক আবিষ্কারের ক্ষেত্রে একটি গুরুত্বপূর্ণ অনুষঙ্গ। অনুমানের মাধ্যমে আমরা বৈজ্ঞানিক গবেষণা শৃঙ্খলায়িত করে নিতে পারি। একটি গবেষণার ফলাফল কেমন হতে পারে বা কি ধরনে পরীক্ষা-নীরিক্ষা করলে একটি কোনো একটি গবেষণা থেকে কাঙ্খিত ফলাফল আসতে পারে তা অনেকসময় পুর্ববর্তী জ্ঞান ও গবেষণাসমূহ হতে বেশ নির্ভুলভাবে অনুমান করা যেতে পারে। এতে অনেক মূল্যবান সময়, অর্থ, শ্রম…
%22%20transform%3D%22translate(.5%20.5)%20scale(1.03516)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23dba100%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(28.24705%2038.31337%20-47.59955%2035.09342%2083.8%20144)%22%2F%3E%3Cellipse%20fill%3D%22%23a2dbff%22%20cx%3D%22169%22%20cy%3D%22255%22%20rx%3D%2271%22%20ry%3D%2276%22%2F%3E%3Cellipse%20fill%3D%22%239a5986%22%20cx%3D%2299%22%20cy%3D%22193%22%20rx%3D%2240%22%20ry%3D%2231%22%2F%3E%3Cellipse%20fill%3D%22%2397e7ff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(3.50025%20176.96539%20-20.86841%20.41276%20166.6%20104.3)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
আসুন মিলেমিশে ভাগাভাগি করে খাই
একটি পুরোনো কৌতুক দিয়ে শুরু করি। একটি রেস্টুরেন্টে ভীষন ভীড় হওয়ায় একই টেবিলে দুজন মানুষ খেতে বসেছেন। ওয়েটার আসা মাত্রই উভয়েই মাছের অর্ডার করলেন। ওয়েটার দুটি প্লেটে করে দুটি মাছ নিয়ে এলেন এবং টেবিলে রাখলেন।বলা বাহুল্য মাছ দুটির আকার একেবার সমান ছিলো না। এই সময় টেবিলে বসা দু’জনের একজন অনেকটা অবচেতনেই বড় মাছের প্লেটটি নিজের…
%22%20transform%3D%22translate(.5%20.5)%20scale(1.03516)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23dba100%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(28.24705%2038.31337%20-47.59955%2035.09342%2083.8%20144)%22%2F%3E%3Cellipse%20fill%3D%22%23a2dbff%22%20cx%3D%22169%22%20cy%3D%22255%22%20rx%3D%2271%22%20ry%3D%2276%22%2F%3E%3Cellipse%20fill%3D%22%239a5986%22%20cx%3D%2299%22%20cy%3D%22193%22%20rx%3D%2240%22%20ry%3D%2231%22%2F%3E%3Cellipse%20fill%3D%22%2397e7ff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(3.50025%20176.96539%20-20.86841%20.41276%20166.6%20104.3)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
গণিতের সৌন্দর্য-পর্ব: ১৭ (শতাংশ বিভ্রাট)
শতকরার বিষয়টি বেশ বিভ্রান্তিকর। স্কুলে পড়ার সময় এই বিষয়ক সমস্যাগুলোর অধিকাংশই ছিলো লাভ-ক্ষতি বিষয়ক। অধিকাংশ সময়ই আমি বুঝতে পারতাম না ক্রয়মূল্যকে ১০০ ধরতে হবে নাকি বিক্রয়মূল্যকে। এতে করে ফলাফল মেলানো অনেক সময় কষ্টসাধ্য হয়ে যেত। এখন স্কুলের সেই সমস্যাগুলোর চেয়েও বিভ্রান্তিকর কিছু শতকরা সমস্যা নিয়ে আলোচনা করব। যেমন: এই সমস্যাটি দেখা যাক। ধরা যাক, আপনি…
%22%20transform%3D%22matrix(2.5%200%200%202.5%201.3%201.3)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23acadaf%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-95.78633%20-9.72962%203.93921%20-38.7808%2059%2033)%22%2F%3E%3Cellipse%20fill%3D%22%23ffef7f%22%20cx%3D%22121%22%20cy%3D%22126%22%20rx%3D%2223%22%20ry%3D%2228%22%2F%3E%3Cellipse%20fill%3D%22%23eaebed%22%20cx%3D%22226%22%20cy%3D%22122%22%20rx%3D%2281%22%20ry%3D%22199%22%2F%3E%3Cellipse%20fill%3D%22%23eaecec%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(-120.4%2061.9%2036.8)%20scale(39.4685%2050.27778)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
গণিতের সৌন্দর্য ১৬: কেন ১ মৌলিক সংখ্যা নয়
প্রাইম নম্বর সম্বন্ধে আমরা সবাই শুনেছি। বাংলায় এইগুলো কে বলা হয়ে থাকে মৌলিক সংখ্যা। নাম থেকেই আমরা বুঝতে পারি প্রাইম হচ্ছে সংখ্যার কিছু মৌলিক ভিত্তি যেগুলোকে ভাঙ্গা হলে আর একই রকম কিছু পাওয়া যায় না এবং যেগুলোর মাধ্যমে অন্য যৌগিক সংখ্যাগুলো তৈরি হয়ে থাকে। এগুলো অনেকটা রসায়নের অলোচিত মৌলিক পদার্থের মতো, মৌলিক পরমানুর বিভিন্ন বিন্যাসের…
%27%20fill-opacity%3D%27.5%27%3E%3Cellipse%20fill%3D%22%23fafeff%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(8.07408%20-98.2069%20715.76857%2058.84689%20288.8%201.5)%22%2F%3E%3Cellipse%20fill%3D%22%23624500%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(124.4%20141.9%20358)%20scale(244.26023%20193.91829)%22%2F%3E%3Cellipse%20fill%3D%22%23abb1ca%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-174.554%20166.22553%20-103.40635%20-108.58737%2026.3%20520.9)%22%2F%3E%3Cellipse%20fill%3D%22%23a88832%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(16.86803%20127.30265%20-90.98171%2012.05538%20325.3%20172.1)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
এন্ডোসিম্বায়োসিস
ধরা যাক, আপনার একটি সুপারপাওয়ার আছে। আর পাওয়ারটি হল সময়কে স্থির করে দেয়া। পরিস্থিতি অনুযায়ী এই পাওয়ার ব্যাবহার এবং প্রয়োজনীয় ব্যাবস্থা গ্রহন, এসব করে সুখেই আছে। “Great power comes with great responsibility” এই ধরনের কোন ফিলোসফি এখনো আপনাকে আক্রান্ত করেনি। তবে কেউ না জানলেও আপনার এই ক্ষমতার সর্বোৎকৃষ্ট ব্যাবহার ঘটে পরীক্ষার হলে। কোন কিছু না…
%27%20fill-opacity%3D%27.5%27%3E%3Cellipse%20fill%3D%22%2390a430%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-34.93113%20-28.80013%2086.6136%20-105.052%2012%2052.8)%22%2F%3E%3Cpath%20fill%3D%22%230a0913%22%20fill-opacity%3D%22.5%22%20d%3D%22M120%20186l85-121.5%2045.7%2032-85%20121.5z%22%2F%3E%3Cellipse%20fill%3D%22%237c7682%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(-62.3%20142.2%20-208.5)%20scale(22.93707%2037.5836)%22%2F%3E%3Cellipse%20fill%3D%22%23939e56%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(23.21729%208.24366%20-17.5163%2049.33259%206%2036.1)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
মাইক্রোস্কোপের নিচের দুনিয়া (মাইক্রোফটোগ্রাফি)
অনেকদিন আগে মাইক্রোস্কোপের নিচে রেখে অ্যামেচার হাতে নিন্মমানের ক্যামেরা দিয়ে কিছু জিনিসের ছবি তুলেছিলাম। বিজ্ঞান ব্লগ হাতড়িয়ে দেখছি সেগুলো আপলোড করা হয় নি। কিংবা বিজ্ঞান ব্লগ যখন ওয়ার্ডপ্রেসের সাবডোমেইন ছিলো তখন আপলোড করা হয়েছিলো, পরে বাদ পড়েছে। আজ সেগুলো নিয়ে এই পোস্ট। আশা করি ছবিগুলো আপনাদের খারাপ লাগবে না। ১. Microchip: CDROM Drive থেকে খুলে…
%27%20fill-opacity%3D%27.5%27%3E%3Cellipse%20fill%3D%22%23d1d1d1%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(-76.8%20103.3%20-37.6)%20scale(45.7324%20118.68817)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(164.2%20130%2064.8)%20scale(51.31104%20263.10683)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(80.16862%2015.5832%20-10.56607%2054.35771%2060.5%20151.5)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(4.23614%20-25.86857%20218.4408%2035.77105%20155.5%209.2)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
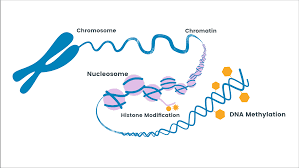
এপিজেনেটিক্স: কিছু সংক্ষিপ্ত ধারনা
ধরা যাক আপনার জন্ম মোটেই স্বাভাবিক জন্ম নয়। আপনার জন্ম হয়েছে কোন এক গোপন ল্যাবরেটরিতে, আপনার এবং আপনার ক্লোনের একসাথে। তারপর এক্সপেরিমেন্টের উদ্দেশ্যে আপনাকে পাঠিয়ে দেয়া হল নানান সমস্যায় জর্জরিত এই বাংলাদেশে, অপরদিকে আপনার ক্লোনকে কোন উন্নত দেশে। আপনি এখানে খাচ্ছেন বিষাক্ত সবজি, ফরমালিন দেয়া মাছ, পানি মেশানো দুধ। অপরদিকে আপনার ক্লোন খাচ্ছে শুধুই অর্গানিক…