সংখ্যা

অয়লার সংখ্যা সমাচার
সংখ্যার সৌন্দর্য আলোচনা করতে গেলে আমাকে এমন আরো হাজারখানেক লেখা তোমাদের সামনে তুলে ধরতে হবে যা আমার উদ্দেশ্য নয়। তবে, সৌন্দর্য উপলব্ধি করার ক্ষেত্রে আজকে তোমাকে একটু ধারনা দিবো। জটিল সংখ্যা নিয়ে সজ্জিত সংখ্যাতত্ত্বের মোটামুটি আমাদের জানা পরিপার্শ্বের সকল কিছু নিয়েই আমার একটা লেখা আগামী কিছুদিনের মধ্যেই তোমরা প্রথম আলো গণিত ইশকুলে পেয়ে যাবে যাতে।…
%22%20transform%3D%22translate(1.6%201.6)%20scale(3.125)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%235f1f74%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(6.94645%2015.93339%20-26.13884%2011.3957%20127.3%20111.9)%22%2F%3E%3Cellipse%20fill%3D%22%23001747%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-12.769%203.75876%20-9.25267%20-31.43256%20110.8%2073.6)%22%2F%3E%3Cellipse%20fill%3D%22%23002753%22%20cx%3D%22106%22%20cy%3D%2259%22%20rx%3D%2217%22%20ry%3D%2217%22%2F%3E%3Cpath%20fill%3D%22%2346357a%22%20d%3D%22M101%20133l3-39%2040%2034z%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
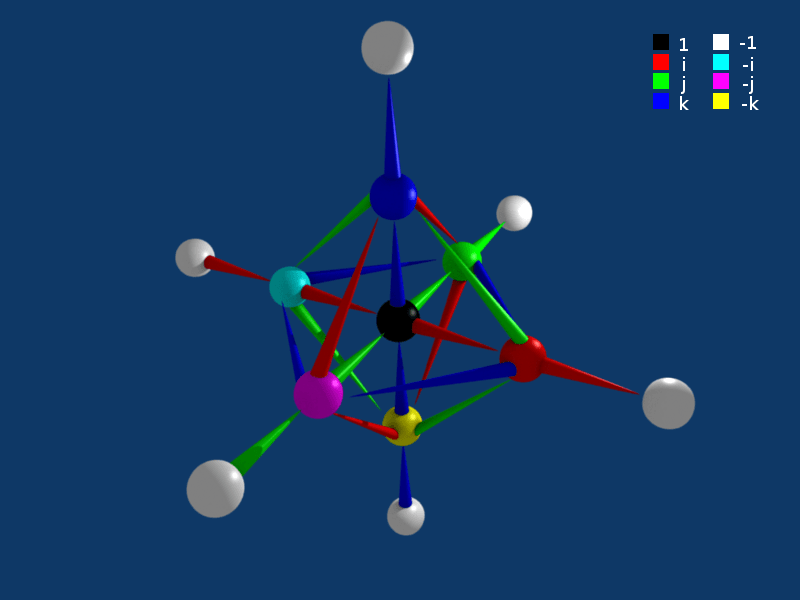
কোয়াটারনিয়ন: সংখ্যার এক অন্যভুবন
ঘড়ির ঘণ্টার কাটা ঘুরানোর কথা চিন্তা করুন। গণিতবিদেরা অনেক আগে থেকেই জানেন কিভাবে এধরনের ঘূর্ণনকে সাধারণ গুণন দিয়ে ব্যাখ্যা করা যায়। খুব সহজ, যে সংখ্যা দিয়ে কাটার অবস্থান প্রকাশ করা হল, সেটাকে আরেকটা ধ্রুবক সংখ্যা দিয়ে গুণ করলে ঘুরে যাবে অবস্থান। এ ঘুর্ণন তো ছিল একটা তলে, মানে দ্বিমাত্রিক ঘুর্ণন। তাহলে এরকম সহজ উপায় দিয়ে…
%27%20fill-opacity%3D%27.5%27%3E%3Cellipse%20fill%3D%22%23393939%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-768.68289%20-1.53466%20.17496%20-87.63517%20480.3%20765.5)%22%2F%3E%3Cellipse%20fill%3D%22%23f8f8f8%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(11.90836%20328.89048%20-995.44145%2036.04262%20458%20291.8)%22%2F%3E%3Cellipse%20fill%3D%22%23454545%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(5.62323%2056.33747%20-222.1033%2022.16886%20475.3%20815)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-51.75173%20-133.9208%20233.59591%20-90.26973%20680.2%202)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
গণিতের সৌন্দর্য্য: পর্ব-৪ (সবচেয়ে বড় সংখ্যাগুলো)
আজ কিছু বড় বড় সংখ্যা নিয়ে আলোচনা করব। আমাদের দৈনন্দিন জীবনে সবচেয়ে বড় যে সংখ্যাটি ব্যবহৃত হয় সেটা হল বিলিয়ন। টাকা গণনার জন্য এই সংখ্যাটি ব্যবহৃত হয়। আমাদের দেশের দু-চারজন মানুষ এই সংখ্যাটি ব্যবহার করেন। দেশের সামগ্রিক অর্থনীতির হিসাবের ক্ষেত্রে আরেকটু বড় সংখ্যা ব্যবহৃত হয়, ট্রিলিয়ন। এই ক্ষেত্রটির বাইরে আমাদের গণনা মিলিয়ন পর্যন্তই সীমাবদ্ধ। ১…