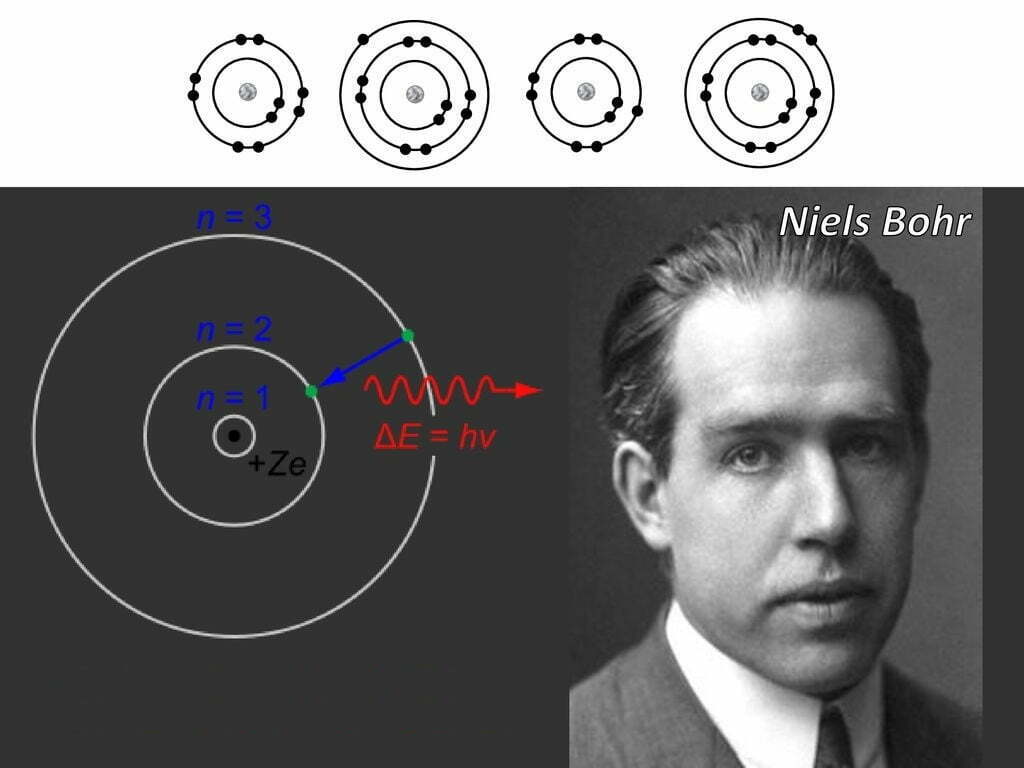
বোরের পরমাণু মডেলে পরমাণুতে ইলেক্ট্রন কিছু নির্দিষ্ট কক্ষপথে ঘুরে। বোর জানতেন যে রাদারফোর্ডের তত্ত্ব ব্যার্থ হয় ম্যাক্সওয়েলের তড়িৎ চুম্বক তত্ত্বের আঘাতে। বোর নিজেও এর সমাধানের পথ খুঁজে পান নি। তখন তিনি ঘোষণা দিয়েছিলেন ইলেক্ট্রন ঐসকল কক্ষপথে থাকার সময় শক্তি শোষণ বা বর্জন করে না। কেনো করে না? তার উত্তর ছিল – পরমাণু জগতে নাকি তড়িৎচুম্বক তত্ত্ব খাটবেই না! ব্যাপারটা জোর করে চাপিয়ে দেয়ার মতো হলেও এটি বেশ গুরুত্বপূর্ণ সিদ্ধান্ত ছিলো। তিনি নিজে প্রথম দিকে প্লাঙ্কের তত্ত্বে আস্থাশীল ছিলেন না। কিন্তু তিনি তার মডেলে বললেন যে ইলেক্ট্রন কিছু নির্দিষ্ট কম্পাঙ্কের আলো শোষণ করে বেশি শক্তিসম্পন্ন কক্ষে যেতে পারে আবার তা বর্জন করে আগের স্থানে ফিরে আসতে পারে। তিনি এসময় ভরবেগকে কোয়ান্টায়িত করে দেন। তিনি বললেন কোন কক্ষে ইলেক্ট্রনের কৌণিক ভরবেগের বেলায় তা একটি ধ্রুবকের গুণিতক হবে। অর্থাৎ কৌণিক ভরবেগ ছিন্নায়িত।
গণিতের ভাষায়, কৌণিক ভরবেগঃ $mvr=\frac{nh}{2\pi}$
এই অদ্ভুত কথাটির কোন ব্যাখ্যাই দেন নি তিনি। আজ আমি বোরের মনের গভীরে ঢুকে জানার চেষ্টা করবো কীভাবে বোর এই ভরবেগের কোয়ান্টায়ন বুঝে ফেললেন।
বোরের পরমাণু মডেল প্রদানের অনেক আগেই হাইড্রোজেন পরমাণুর জন্য বর্ণালী সিরিজ আবিষ্কার হয়েছিল। এক্ষেত্রে, $m$ হল বর্ণালী রেখার লাইন নম্বর আর $n$ এর মান বিভিন্ন বর্ণালী সিরিজ নির্দেশ করে। যেমন, $n=2$ হলে তা বামার সিরিজ নির্দেশ করে।
রিডবার্গ ধ্রুব $R$ হলে, বিকিরিত বর্ণালীর তরঙ্গদৈর্ঘ্য $\lambda$ হলে,
$$ \frac{1}{\lambda}=R\left(\frac{1}{n^2}- \frac{1}{m^2} \right) \label{i} \tag{i} $$ এখানে $m, n$ পূর্ণসংখ্যা ও $m>n$ হয়।
সম্ভাবত মেধাবী বোর এই সমীকরণ থেকে বুঝতে পারেন, আলো $m$ তম শেল থেকে $n$ তম শেলে নেমে আসলে এই বিকিরণ ঘটে।
তিনি আরও বুঝলেন যে $n$ তম শেল থেকে $m$ তম শেলে যেতে একই শক্তি শোষণ করতে হবে। আর নির্দিষ্ট শেলে থাকাকালীন কোন শক্তির শোষণ বা বিকিরণ ঘটবে না কারণ ক্লাসিক্যাল ফিজিক্স পরমাণু জগতের জন্য নয় (ক্লাসিক্যাল ফিজিক্সের মত মানলে পরমাণুর ইলেক্ট্রন নিউক্লিয়াসে পড়ে যাবে)। অর্থাৎ বোর বুঝলেন পরমাণুর বর্ণালী থেকেই কেবল পরমাণুর রহস্য সমাধা করা সম্ভব। আর এই পর্যায়ে তিনি বুঝতে পারেন যে প্লাঙ্কের তত্ত্ব সঠিক দিশা দিতে পারে।
এখন, সমীকরণ \eqref{i} এ $m=\infty$ বসালে $n$ তম শেলের আয়নিকরণ বিভব এর সমান শক্তিবিশিষ্ট আলোর তরঙ্গদৈর্ঘ্য পাওয়া যাবে কেননা আয়নিক বিভব মানে কোন শেলের ইলেক্ট্রনকে অসীমে নিয়ে যেতে দরকারী শক্তি।
$$ \frac{1}{\lambda}=\frac{R}{n^2} \\ E=- \frac{hc}{\lambda} $$
এখানে ঋণাত্মক চিহ্ন বুঝাচ্ছে যে এটি পটেশিয়াল কূপে আটকে আছে। ধরুন, একটি কুয়ায় আপনি $-5\mathrm J$ শক্তিতে পড়ে আছেন। তাহলে কুয়া থেকে বের হতে গেলে আপনার $+5 \mathrm J$ শক্তি লাগবে।
তাহলে $n$ তম শক্তিস্তরের শক্তি
$$ E=- \frac{hcR}{n^2} \label{ii} \tag{ii} $$
এবার দেখা যাক, আমাদের ক্লাসিক্যাল ফিজিক্স কী বলে!
ক্লাসিক্যাল ফিজিক্স বলে ইলেক্ট্রনকে ঘুরাচ্ছে প্রোটনের আকর্ষণ বল। আর এজন্য স্থিতিশক্তি ও গতিশক্তি দুটোই থাকবে। আর কলনবিদ্যা (ক্যালকুলাসের বাংলাই কলনবিদ্যা!), কুলম্ব সূত্র এবং নিউটনীয় বলবিদ্যা দুটোই প্রয়োগ করলে পাই,
গতিশক্তি, $ K=\frac {ke^2}{2r}$,
স্থিতিশক্তি, $U=\frac {-ke^2}{r} $
এখানে $k$ হল কুলম্বের ধ্রুবক, শুন্যস্থানে যার মান $9\times 10^9 \, \mathrm{Nm^2/C^2}$
তাহলে মোট শক্তি $$E=K+U=\frac{-ke^2}{2r} \label{iii} \tag{iii} $$
\eqref{ii} এর সাদৃশ্য টেনে বলতে পারি $$r_n= \frac{k(ne)^2}{hcR} \label{iv} \tag{iv} $$
এটাই বোরের মডেলের অনুরূপ n তম কক্ষপথের ব্যাসার্ধের রাশিমালা। যেখানে, $n=1,2,3, \dots$
আবার যেহেতু কুলম্ব বল ইলেক্ট্রনকে ঘুরায়, অর্থাৎ
$$ \frac {mv^2}{r}= k\left(\frac{e}{r} \right)^2 $$ এ $r$ এর মান বসিয়ে $v$ এর রাশিমালা পাওয়া যায়। $m,v,r$ গুণ করে দেখানো যাবে যে $mvr$ (কৌণিক ভরবেগ) কেবল $n$ এর সমানুপাতিক। আর এই ধ্রুবকের মান বের করে দেখুন তা $\frac{h}{2\pi}$ এর সমান।
তাহলে দেখা যাচ্ছে বেশ সহজে বর্ণালী সিরিজ থেকেই বোরের তত্ত্ব থেকে প্রাপ্ত সমীকরণ পাওয়া গেল।
সম্ভাবত নিলস বোর এই কাজটিই করেছিলেন।
আর এটি সম্ভব হয়েছিল বোর অসম্ভব মেধাবী বলেই। নাহলে কেবল বর্ণালী সিরিজ থেকেই এসকল রাশিমালা চিন্তা করা সহজ নয়। বোর অবশ্য উল্টোভাবে উপস্থাপন করেছেন, তাই রহস্যটা ধরতে পারা যায় নি। আপনারাই বলুন, কৌণিক ভরবেগের কোয়ান্টায়ন তো হাওয়ায় উড়ে আসে নি!
পরে অবশ্য ডি-ব্রগলির তত্ত্বে এর ব্যাখ্যা পাওয়া গিয়েছিলো। অনুরূপ নীতিও একই ফলাফল দেয়।
Leave a Reply