প্রতিসাম্য এবং এর ভাঙ্গণ (প্রথম পর্ব)

প্রতিসাম্য (Symmetry) কি ? এই প্রশ্নটির যদি একটি সাধারণ উত্তর খুঁজি, তাহলে উত্তরটি হবে কিছুটা এই রকম –

‘প্রতিসাম্য দেখা যায় এমন কিছু বস্তুর মধ্যে যাদের কে একটি নির্দিষ্ট নিয়মে সমান দুইটি অংশে ভাগ করলে ভাগ করা দুইটি অংশের পরস্পরের মধ্যে সদৃশ পাওয়া যায়’ ।

এই ধর্মটি দেখা যায় নির্দিষ্ট কিছু জ্যামিতিক কাঠামোতে । যেমন ঘনক, গোলক, বৃত্ত, সামন্তরিকের ইত্যাদি ক্ষেত্রে-

চিত্রঃঘনকের প্রতিসাম্য

আসলে প্রতিসাম্য দ্বারা আমরা বুঝতে পারি (প্রতিসাম্য নিয়ে এসেছে) বিজ্ঞানে সাম্যতা, অনুপাত, এবং একতান যা বিজ্ঞানকে করেছে আরো সুন্দর । শুধু বিজ্ঞানেই না এটা প্রায় দেখা যায় আর্টশিল্পে, আর্কিটেকচারে এবং সংগীতে ।

চিত্রঃ প্রতিসাম্য আর্কিটেকচারে

আমরা শুধু কোন বস্তুর বা আকৃতির প্রতিসাম্যের দিক নিয়ে আলোচনা করবো ।

প্রতিসাম্যের বিভিন্ন সংজ্ঞা আছে, তবে আমরা বিজ্ঞান ও গণিতের দিক দিয়ে সংজ্ঞাটা কি হতে পারে তা দেখবো । পদার্থবিদরা প্রতিসাম্যের সংজ্ঞা দেয় এই ভাবেঃ “কোন বস্তুর রূপান্তরের(Transformation) পরও যদি বস্তুটি অপরিবর্তিত থাকে তাহলে একে প্রতিসাম্য বলে ”। আরেকটু বিস্তারিত ভাবে বললে একটি সিস্টেমকে বিভিন্ন ভাবে রূপান্তর( Transformation)করা সম্ভব, এবং এই রূপান্তরের পরেও যদি সিস্টেমটি একই ধর্ম প্রদর্শন করে অর্থাৎ সিস্টেমটি যদি অপরিবর্তিত থাকে তাহলে একেই বলা হবে প্রতিসাম্য । অপরিবর্তনের নীতি এবং প্রতিসাম্যের মিলের দিক দিয়ে চিন্তা করলে কয়েক ধরনের রূপান্তর হয় ।

রূপান্তরএর প্রকারভেদ

বিচ্ছিন্ন (Discrete)বা অবিচ্ছিন্ন (Continuous), জ্যামিতিক(Geometrical) বা আভ্যন্তরীণ(Internal), গ্লোবাল(Global) অথবা লোকাল(Local) ।

যখন বিচ্ছিন্ন পদক্ষেপে প্রতিফলন সংঘটিত হয় তখন স্থান-কালের রূপান্তর এবং ঘূর্ণন হচ্ছে “অবিচ্ছিন্ন প্রতিসাম্যের রূপান্তর”এর উদাহরণ, । প্রকৃতি হচ্ছে প্রাথমিক স্তর, যেখানে গেজ-রূপান্তরে সমীকরণ দ্বারা বর্ণনা করে আভ্যন্তরীণ অপরিবর্তন, লোকাল ও অবিচ্ছিন্ন রূপান্তর সমূহকে ।  গ্লোবাল এবং লোকাল প্রতিসাম্য নিয়ে কিছু আলোচনা করা যাক ।

গ্লোবাল এবং লোকাল প্রতিসাম্যঃ

গ্লোবাল এবং লোকাল প্রতিসাম্য রূপান্তর সম্পর্কে আলোচনা করার কারণ হচ্ছে, এই রূপান্তর দুটি আমাদের হিগস বোসন, গোল্ডস্টোন বোসন এবং W ও Z এর ভর সম্পর্কে বুঝার জন্য প্রয়োজন হয় ।

১৯৫৪ সালে ইয়ং এবং মিলস্ গেজ-তত্ত্বের প্রথম প্রবর্তন করেন । আসলে এই দুই   বিজ্ঞানীর উদ্দেশ্য ছিল এমন একটি তত্ত্ব তৈরী করা যেখানে গ্লোবাল প্রতিসাম্য কে লোকাল প্রতিসাম্যেনিয়ে আসা যায় । এর ফলে স্থান-কালের বিভিন্ন বিন্দুতে স্বাধীনভাবে গ্লোবাল রুপান্তর করা সম্ভব হবে ।

যদি আপনারা Jumper মুভিটা দেখে থাকেন তাহলে দেখবেন নায়ক এক জায়গা হতে আরেক জায়গায় চলাফেরা করে বাতাসে অদৃশ্য হয়ে । ধরুন Jumper মুভির নায়ক আর শুভ নামের একজন তরুন আমাদের বাংলাদেশের সংসদ ভবনের সামনে দাঁড়িয়ে আছে । এই দুইজন কে ঢাকা বিশ্ববিদ্যালয়ের  টি.এস.সি যেতে বলা হল । Jumper মুভির নায়কের ক্ষেত্রে আমরা দেখতে পাব সে “বাতাসে গহ্বরে” অদৃশ্য হয়ে মুহূর্তের মধ্যে টি.এস.সি তে হাজির হয় । পদার্থ বিজ্ঞানের অপভাষায়, ইহা “Global conservation of man ” এর সাথে মিল রয়েছে, এর অর্থ হচ্ছে (Jumper মুভির) যেকোনো সময় নায়কের ভূমণ্ডলের যে কোন স্থানেই তার অস্তিত্ব রয়েছেঃ একবার সংসদ ভবনের সামনে পর মুহূর্তে আবার টি.এস.সি তে । কিন্তু এটা কি সাধারণ মানুষের ক্ষেত্রে প্রযোজ্য? অবশ্যই না । ধরুন (সংসদ ভবনের সামনে দাঁড়ানো) শুভর কথা । শুভর ক্ষেত্রে আমরা দেখব সে হেটে হেটে (কারণ ঢাকায় তখন হরতাল চলছে, বিরোধী দলের কর্মীরা যানবাহন দেখলেই হয় ভাঙ্গে না হয় পোড়ায় ) অর্থাৎ একটি একটি পদক্ষেপ ফেলে  আস্তে আস্তে টি.এস.সি তে যেতে হবে (Jumper মুভির নায়কের মত “বাতাসে গহ্বরে” অদৃশ্য না হয়ে ) । পদার্থ বিজ্ঞানের অপভাষায়, এটাকে “Local conservation of man” বলা হয় । এই “বাতাসের গহ্বর” আমরা কণা পদার্থ বিজ্ঞানের ক্ষেত্রে এর উপস্থিতি আছে । যা কণা সৃষ্টি করতে পারে (Jumper মুভির) নায়কের মত যে কোন সময় । “Global conservation ” যেমন সত্য ঠিক তেমনি  “Local conservation ”ও সত্য । তবে “Global conservation”এর উদাহরণে বাতাসের অদৃশ্য হবার ক্ষেত্রে অনেক সীমাবদ্ধতা রয়েছে, এটা মূলত “বাতাসের গহ্বরে” অদৃশ্য হতে নিষেধ করে ।

নাম্বুর মডেলে গোল্ডস্টোনের উদাহরণে আমরা দেখতে পাই, গ্লোবাল প্রতিসাম্য ভঙ্গের কারণে বলটি(Ball) ঘুরে ওয়াইন বোতলের (মেক্সিকান টুপির) নিম্নস্তরে । ভরহীন গোল্ডস্টোন বোসন ওয়াইন বোতলের নিম্নস্তরে প্রত্যেক বিন্দু অতিক্রম করে ঘুরে  । যখন পদার্থ বিজ্ঞানে গ্লোবাল প্রতিসাম্য কোন নীতি বৈধ করে, তখন লোকাল মিথস্ক্রিয়া কণার অনেক ক্ষেত্রেই মৌলিক গতিবিদ্যা নিয়ন্ত্রন করে ।  লোকাল গেজ রূপান্তরের অপরিবর্তন বাধ্য করে ইলেকট্রিক চার্জের তত্ত্বের জন্য যা পরোক্ষভাবে বুঝায় যে ইলেকট্রিক চার্জ হচ্ছে সংরক্ষণশীল এবং এখানে একটি বল রয়েছে আর তা হচ্ছে ইলেকট্রিক ভাবে চার্জিত কণার ক্ষেত্রে ইলেক্ট্রোম্যাগনেটিক বল । উদাহরণ স্বরূপ হাইড্রোজেন পরমাণুতে রয়েছে একটি ইলেকট্রন ও একটি প্রোটন এরা পরস্পর ইলেকট্রিক চার্জ দ্বারা আকর্ষিত । কোয়ান্টাম ক্ষেত্র তত্ত্ব মতে এদের দুইয়ের মধ্যে ফোটন আদান-প্রদানের ফলাফল হচ্ছে এই আকর্ষণ । প্রথমে এখানে বিশেষ স্থানের ইলেকট্রন ও ফোটনের মধ্যে, একটি লোকাল মিথস্ক্রিয়া সংঘটিত হয়েছিল; পরে ফোটন মধ্যবর্তী স্থানে ভ্রমন করে এবং মিথস্ক্রিয়ার মাধ্যমে পরবর্তী স্থানে থাকা প্রোটনকে  বল (Force) সরবারহ করে ।

এখানে ইলেক্ট্রোম্যাগনেটিক মিথস্ক্রিয়াকে লোকাল প্রতিসাম্য নিয়ন্ত্রণ করছে ।  লোকাল প্রতিসাম্য রূপান্তরের একটি উদাহরণ হচ্ছে কোন বস্তুকে ঘুরানোর ফলে যদি বস্তুটি একই ধর্ম প্রদর্শন করে । পরে বিস্তারিত আলোচনা করা হয়েছে ।

আমরা আগেই বলেছি লোকাল প্রতিসাম্যের একটি ফলাফল হচ্ছে ইলেক্ট্রোম্যাগনেটিক বল, যা ফোটনের উৎপত্তির কারণ । তাই প্রস্ন আসে কি হবে যদি লোকাল প্রতিসাম্য স্বতঃস্ফূর্তভাবে ভাঙ্গে ? গ্লোবাল প্রতিসাম্য যখন স্বতঃস্ফূর্তভাবে ভাঙ্গে তখন প্রয়োগ করা হয় গোল্ডস্টোন উপপাদ্য কিন্তু  লোকাল প্রতিসাম্য ধারণ করে এমন একটি সমাধান যা পরিহার করে তার উপপাদ্যকে । লোকাল তত্ত্ব হচ্ছে গ্লোবাল প্রতিসাম্য হতে সহজ, এটা প্রকাশ করে যে ভরহীন গোল্ডস্টোন বোসনের অস্তিত্বের কোন প্রয়োজন নেই । লোকাল প্রতিসাম্য ভরহীন ভেক্টর গেজ বোসন সৃষ্টি করে । যদি এই লোকাল প্রতিসাম্য স্বতঃস্ফূর্তভাবে ভাঙ্গে, তাহলে এই ভরহীন ভেক্টর গেজ বোসন, গোল্ডস্টোন বোসনকে খেয়ে ফেলে নিজে (ভরহীন ভেক্টর গেজ বোসন) ভর লাভ করে । আর তাই ভরহীন গোল্ডস্টোন বোসন অদৃশ্য হয়ে যায় । অর্ধ শতাব্দী যাবত গবেষণার মাধ্যমে কণা পদার্থ বিজ্ঞানে এই প্রমাণটি করা হয়েছে ।

অর্থাৎ লোকাল প্রতিসাম্য ভঙ্গের কারণে গেজ ক্ষেত্র ভর প্রাপ্ত হয়, এবং ভরহীন স্পিন-শূন্য বিশিষ্ট গোল্ডস্টোন বোসন ভরবিশিষ্ট এবং স্পিন-এক পূর্ব-পশ্চিম পোলারাইজড্ যুক্ত W ও Z বোসন কণায় পরিবর্তিত হয় । আসলে W ও Z বোসন হচ্ছে ফোটনের মত গেজ কণা, তবে এদের মধ্যে মূল পার্থক্য হচ্ছে ফোটন কোন হিগস কণা তথা গোল্ডস্টোন বোসন কণার সাহায্য ছাড়াই পুনঃসাধারণীকরণ করা যায় (মজা করে বলা যায় ফোটন কোন গোল্ডস্টোন বোসন খায় না তাই এর ভর শূন্য) কিন্তু W ও Z বোসন পুনঃসাধারণীকরণ করতে তিনটি (H+,H- ও H0 ) হিগস কণা তথা গোল্ডস্টোন বোসন কণার প্রয়োজন হয় (মজা করে বলা যায় W+, W- ও Z0 গোল্ডস্টোন বোসন খায় তাই এদের ভর আছে )।

যাইহোক প্রতিসাম্যের প্রকারভেদ নিয়ে কিছু বলা যাক পরে নাহলে এর ভাঙ্গন (Symmetry Breaking) সম্পর্কে আলোচনা করব । প্রতিসাম্য যে খুবই গুরুত্বপূর্ণ বিষয় তা আমরা প্রমাণ পাই প্রকৃতির সর্বস্তরে । প্রতিসাম্য আমরা দেখতে পাই যে কোন স্থানে, গাছের পাতার আকৃতিতে, আমাদের শরীরের গঠনে, এবং গণিতের সমীকরণে যা চালনা করে আমাদের জানা প্রকৃতির সূত্রগুলোকে । প্রকৃতপক্ষে আমাদের মহাবিশ্বের মৌলিক আলোচ্য বিষয় হচ্ছে এই প্রতিসাম্য এবং পদার্থবিদরা যখন কোন নতুন তত্ত্ব সৃষ্টি করে তখন প্রতিসাম্যের কথা মাথায় রেখে সৃষ্টি করে । যখন কোন কিছু ব্যাখ্যা করার জন্য দুইটি সমীকরণের সম্ভাবনা দেখা দেয়, তখন যেই সমীকরণটি প্রতিসাম্য সম্পন্ন হয় তাই গ্রহণ করেন কারণ এই সমীকরণটি সৌন্দর্যতা রক্ষা করে ।

চিত্রঃপ্রকৃতিতে প্রতিসাম্য

প্রতিসাম্য এর প্রকারভেদ

বিভিন্ন দিক দিয়ে চিন্তা করলে প্রতিসাম্য কয়েক প্রকার হতে পারে তবে আমরা জ্যামিতিক দিয়ে চিন্তা করবো । জ্যামিতিক দিয়ে চিন্তা করলে প্রতিসাম্য তিন প্রকারঃ

১) Reflection

২) Translational এবং

৩) Rotational

Reflection:

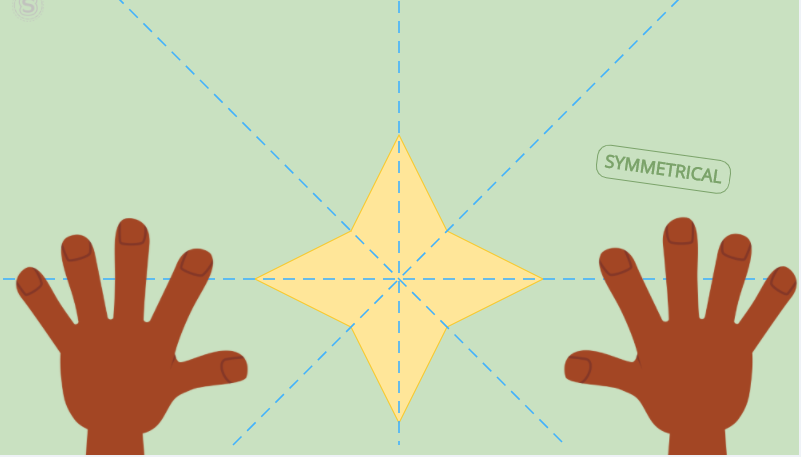
আমরা সবচেয়ে বেশি পরিচিত Reflection(প্রতিফলন) প্রতিসাম্যের সাথে । নিচের চিত্রগুলোতে Reflection Symmetry এর উদাহরণ দেওয়া হল । এদের আকৃতি একই থাকে যদি সরল রেখার এক পাশ থেকে প্রতিফলিত করি । এই সরল রেখাকে বলা হয় Symmetry axis ।

চিত্রঃReflection Symmetry

Translational:

Translational Symmetry একটি সিস্টেম কে বর্ণনা করে এই ভাবে যে, যখন একটি নির্দিষ্ট রুপান্তর এই সিস্টেমে সংঘটিত হবে তখন সিস্টেমটি অপরিবর্তিত (Invarient) থাকবে । এর অর্থ হচ্ছে কোন বস্তুর আকৃতির পরিবর্তন হবে না যখন বস্তুটির কোন রূপান্তর হবে (যেমন Rotation এবং Reflection ছাড়া বিভিন্ন  মাত্রায় বস্তুটিকে নাড়ানো হল ) । ৪ মাত্রার (৩টি স্থান এবং ১টি কালের মাত্রা)যে কোন মাত্রায় বস্তুটিকে নাড়ানো হল, কি এখনো বুঝেন নাই? আচ্ছা তাহলে এই ভাবে বললে কেমন হয় । ধরুন আপনার ডান হাতে একটি কলম আছে, এই কলমটিকে আপনি বাম হাতে নিলেন এর ফলে কলমটির স্থানের এবং কালের রূপান্তর হল কিন্তু কলমটির কিন্তু আগে যেমন ছিল বাম হাতে আসার পর একই রকম রয়েছে । নিশ্চয় এখন বুঝেছেন Translational Symmetry কি ।

চিত্রঃ Translational Symmetry

Rotational:

আমাদের এই মহাবিশ্বে বস্তুর Translational Symmetry হচ্ছে একটি সাধারণ বিষয় । যে কোন বস্তুই ৩৬০ ডিগ্রি কোণে ঘুরতে পারে, এখন এই বস্তুটি নির্দিষ্ট কোণে ঘুরার পর যদি দেখতে একই রকম লাগে তাহলে আমরা একে Translational Symmetry বলব । চিত্রে আমরা snowflake দেখতে পারছি, এই snowflake টি হচ্ছে    sixfold symmetry অর্থাৎ snowflake টিকে একটি নির্দিষ্ট বিন্দু হতে (৩৬০/৬=) ৬০ ডিগ্রি কোণে ঘুরালে snowflake টিকে আবার একই রকম দেখা যাবে ।

ঠিক একই রকম Isle of Man কে (৩৬০/৩)= ১২০ ডিগ্রি কোণে ঘুরালে আবার একই রকম দেখা যাবে । তারমানে আমরা বলতে পারি Isle of Man  হচ্ছে  threefold symmetry ।

চিত্রঃ Isle of Man

চলবে ………

সূত্রঃ

১.প্রতিসাম্য উইকি

২. Symmetry by Leon M.Lederman

৩.The Infinity Puzzle by frank close

৪.An Introduction to the Standard Model of Particle Physics by W.N.Cottingham & D.A.Greenwood