গণিতে প্রচুর পরিমাণে কন্ডিশনাল স্টেটমেন্ট ব্যবহৃত হয়, আমরাও আমাদের কথার মাঝে প্রচুর কন্ডিশনাল স্টেটমেন্ট ব্যবহার করি। যেমন, ‘যদি আজ বৃষ্টি নামে তবে বাংলাদেশ জিতে যাবে’, ‘যদি কোন আয়তের দুটি সন্নিহিত বাহু সমান হয় তবে এটি একটি বর্গ’। আমরা উদাহরণগুলো থেকে কন্ডিশনাল স্টেটমেন্টের কিছু বৈশিষ্ট্য খেয়াল করি- প্রতিটি স্টেটমেন্টের গঠন এরকম: ‘যদি Statement1 তবে Statement2’ (‘If Statement1 then Statement2’), এখানে দুটো Statement ‘If…then..’ দিয়ে যুক্ত হয়েছে। মানে দুটো সিম্পল স্টেটমেন্ট মিলে কমপ্লেক্স আরেকটা স্টেটমেন্ট। Statement1 কে বলা হয় Hypothesis, Statement2 কে বলা হয় Conclusion পুরো কন্ডিশনাল স্টেটমেন্টটি মিথ্যা হবে যদি Hypothesis সত্য হলেও Conclusion মিথ্যা হয়। যেমন ধরুন আমরা বললাম ‘যদি বিস্তারিত
সৈয়দ ইমাদ উদ্দিন শুভ
ক্লাসিক্যাল মেকানিক্স পর্ব-২: গ্যালিলিয়ান ট্রান্সফর্মেশন ও স্পেসটাইম ডায়াগ্রাম
আগের পর্বে আমরা নিউটনের গতিসূত্র কীভাবে আসলো, সূত্রগুলো কখন খাটে এসব নিয়ে আলোচনা করেছি। আমরা এটা দেখেছি যে নিউটনের সূত্রগুলো একটা বিশেষ ফ্রেমে খাটে, যাদের ইনারশিয়াল ফ্রেম বা গ্যালিলিয়ান ফ্রেম বলা হয়। আজকে আমরা এই বিশেষ ফ্রেম নিয়ে সবিস্তর আলোচনা করবো। আর এর সাথে আমরা আজকে স্পেসটাইম ডায়াগ্রামের সাথে পরিচিত হবো। ক্লাসিক্যাল মেকানিক্স সিরিজের শেষের দিকে আমরা যখন আপেক্ষিকতার বিশেষ তত্ত্বের সাথে পরিচিত হবো, তখন আমাদের এই লেখার ধারণা দারুণ কাজে দেবে বলে আমার বিশ্বাস। ধরুন, আপনি একটা ট্রেনে বসে আছেন, আপনি কিন্তু ট্রেনের ভেতর আপনার ট্রেন সাপেক্ষে স্থির। চারদিক অন্ধকার। আপনি বাইরে তাকালে শুধু অন্য একটা ট্রেন দেখতে পারবেন, বিস্তারিত
ক্লাসিক্যাল মেকানিক্স পর্ব-১: নিউটনের গতিসূত্রের ইতিহাস
আমরা স্কুলে ক্লাস নাইনে ওঠার পরপরই নিউটনের গতিসূত্রের সাথে পরিচিত হই। ১৬৮৭ সালে প্রকাশিত Philosophiæ Naturalis Principia Mathematica বইতে ব্রিটিশ বিজ্ঞানী স্যার আইজ্যাক নিউটন তিনটি গতিসূত্র প্রকাশ করেন, যা পদার্থবিজ্ঞানের ইতিহাসে অত্যন্ত গুরুত্ববহ একটি ঘটনা। নিউটনের তিনটি গতিসূত্রই মূলত বিন্দু ভর (point mass) এর জন্য। বিন্দু ভর মানে এর কোন সাইজ নেই, এটি একটি বিন্দু যার ভর আছে। পুরো ব্যাপারটাই তাত্ত্বিক, কেননা এরকম কোন কিছু আমরা আশে পাশে দেখি না। কিন্তু এই বিন্দু ভরের একটা গাণিতিক সুবিধে আছে। একটা বড় বস্তুতে বল প্রয়োগ করলে কোথায় বল প্রয়োগ করেছি তার ওপর সবকিছু নির্ভর করে। বলের প্রভাবে অনেক সময় বস্তু ঘুরে, অনেকসময় বিকৃত হয়, বিস্তারিত
অসীম ধারার গল্প
নবম দশম শ্রেণীতে আমাদের অসীম ধারার সাথে পরিচয় ঘটে। বিশেষ করে গুণোত্তর ধারার সাথে পরিচয় হওয়ার দিন কয়েক পরেই আমরা শিখি যে , ½ + ¼ + ⅛ +……………=1 সাধারণভাবে এটা আমরা গাণিতিকভাবে মেনে নেই, কিন্তু কেনো অসীম পর্যন্ত নিয়ে সমষ্টি 1 পাওয়া যায়, তা বোঝার চেষ্টাও করি না। দেখা যাক আমরা কী শিখি, আমরা শিখি যে, s=½ + ¼ + ⅛ +…………… উভয়পক্ষে ½ গুণ দিয়ে পাই, ½s=¼+⅛+………….. যেহেতু অসীম ধারা, বিয়োগ দিলে পাই, ½s=½ বা, s=1 আর এখানে শেষ পদ বিবেচনায় আনাই হয় নি, কারণ এই ধারার পদগুলো ক্রমশ ছোট হতে হতে অসীমে গিয়ে শুন্যের দিকে ধাবিত হবে। বিস্তারিত
গৌনিক ও গামাবাবুর গল্প
গৌনিক! এটা আবার কী জিনিস? এটা আর কিছুই না, factorial এর বাংলা ! 😛 n factorial কে n! দিয়ে প্রকাশ করা হয়। n! হল প্রথম n সংখ্যক স্বাভাবিক সংখ্যার গুনফল। তার মানে, 1!=1 2!=2 × 1=2 3!=3 × 2 × 1=6 4!=4 × 3 × 2 × × 1=24 5!=5 × 4 × 3 × 2 × 1=120 …………………. ………… এরকম চলতে থাকবে। খেয়াল করুন, উপরের উদাহরণ থেকে সহজেই বুঝা যায় যে, n!=n.(n-1)! এখন n=1 হলে উপরের সম্পর্কে 0! এসে পড়ে। আর এটি সংজ্ঞায়িত না। কাজেই উপরের সমীকরণ যদি n=1 এর জন্য সত্য হতে হয় তবে 0!=1 হতে বিস্তারিত
এক চলকবিশিষ্ট বহুপদীর উৎপাদকে বিশ্লেষণ
এক চলক বিশিষ্ট বহুপদী হল বীজগাণিতিক রাশি, যার প্রতিটি পদ C.xⁿ আকারের। যেখানে , n∈ℤ+, আর C হল ধ্রুব। আমার আলোচনায় n≤4 থাকবে আর C পূর্ণসংখ্যা। বহুপদীতে সসীম সংখ্যক পদ থাকবে। একটি পদ থাকলেও বহুপদী হয়। উদাহরণস্বরূপ, 2x³-3 একটি বহুপদী, এর দুটি পদ 2x³ এবং -3 বহুপদীর উৎপাদকে বিশ্লেষণ হল বহুপদীকে একাধিক বহুপদীর গুণফল আকারে প্রকাশ। এখন, n=2 হলে বহুপদীর উৎপাদকে বিশ্লেষণ আমরা সবাই জানি। তবুও একটু দেখা যাক, ax²+bx+c এর উৎপাদকে বিশ্লেষণ করতে হবে। a,b,c এখানে পূর্ণসংখ্যা ও সহমৌলিক। এবার ax²+bx+c=0 এর মূলগুলো যদি মূলদ হয়, তবে উৎপাদকে বিশ্লেষণ সম্ভব। আর এর শর্ত b²-4ac পূর্ণবর্গ হতে হবে। এখন, ধরা বিস্তারিত
কথা ছাড়া প্রমাণ: গণিতের সৌন্দর্য
গণিত এক অবাক করা সুন্দরী। এর প্রতিটি বাঁকে রয়েছে অপূর্ব এক মায়া। আজ আমরা গণিতের এক ধরনের প্রমাণের কথা বলব, যার জন্য কোন কথার প্রয়োজন হয় না। শুধু ছবি থেকেই প্রমাণিত হয়ে যায়! সমীকরণের যদি প্রয়োজন হয়ও তবুও তা মাত্র কয়েক লাইন। সবচেয়ে বড় কথা হচ্ছে, এ ধরনের প্রমাণ আমাদের শেখায় কীভাবে গণিতকে অনুভব করতে হয়। গণিতের বিমূর্ত সূত্র, উপপাদ্যসমূহ তখন জীবন্ত হয়ে শিরা-উপশিরায় বইতে থাকে। এ ধরনের প্রমাণকে বলা হয় proof without words, বাংলায় কথা ছাড়া প্রমাণ। মাধ্যমিক গন্ডির শুরুতেই আমাদের সাথে পরিচয় হয় (a+b)²=a²+2ab+b² সূত্রটির! কিন্তু কয়জন তার প্রমাণ পারে? যারা পারে তাদের মধ্যে কয়জনই বা এর বিস্তারিত
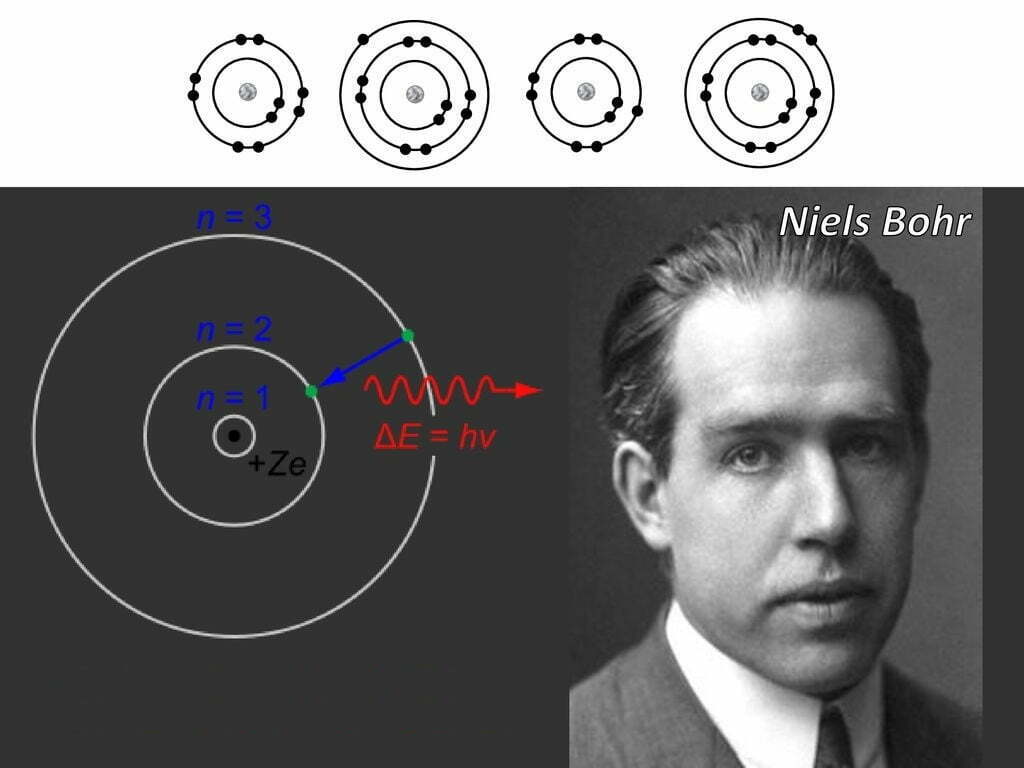
বোর মডেলের অন্তরালে
বোরের পরমাণু মডেলে পরমাণুতে ইলেক্ট্রন কিছু নির্দিষ্ট কক্ষপথে ঘুরে। বোর জানতেন যে রাদারফোর্ডের তত্ত্ব ব্যার্থ হয় ম্যাক্সওয়েলের তড়িৎ চুম্বক তত্ত্বের আঘাতে। বোর নিজেও এর সমাধানের পথ খুঁজে পান নি। তখন তিনি ঘোষণা দিয়েছিলেন ইলেক্ট্রন ঐসকল কক্ষপথে থাকার সময় শক্তি শোষণ বা বর্জন করে না। কেনো করে না? তার উত্তর ছিল —- পরমাণু জগতে নাকি তড়িৎচুম্বক তত্ত্ব খাটবেই না! ব্যাপারটা জোর করে চাপিয়ে দেয়ার মতো হলেও এটি বেশ গুরুত্বপূর্ণ সিদ্ধান্ত ছিলো। তিনি নিজে প্রথম দিকে প্লাঙ্কের তত্ত্বে আস্থাশীল ছিলেন না। কিন্তু তিনি তার মডেলে বললেন যে ইলেক্ট্রন কিছু নির্দিষ্ট কম্পাঙ্কের আলো শোষণ করে বেশি শক্তিসম্পন্ন কক্ষে যেতে পারে আবার তা বর্জন বিস্তারিত