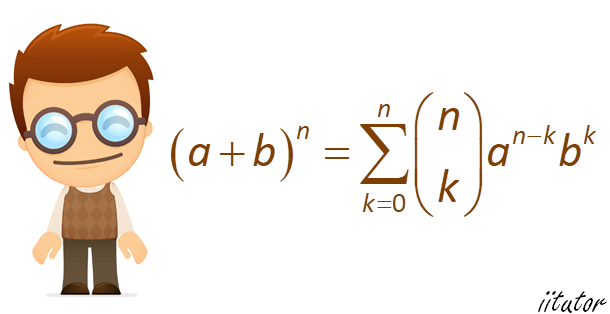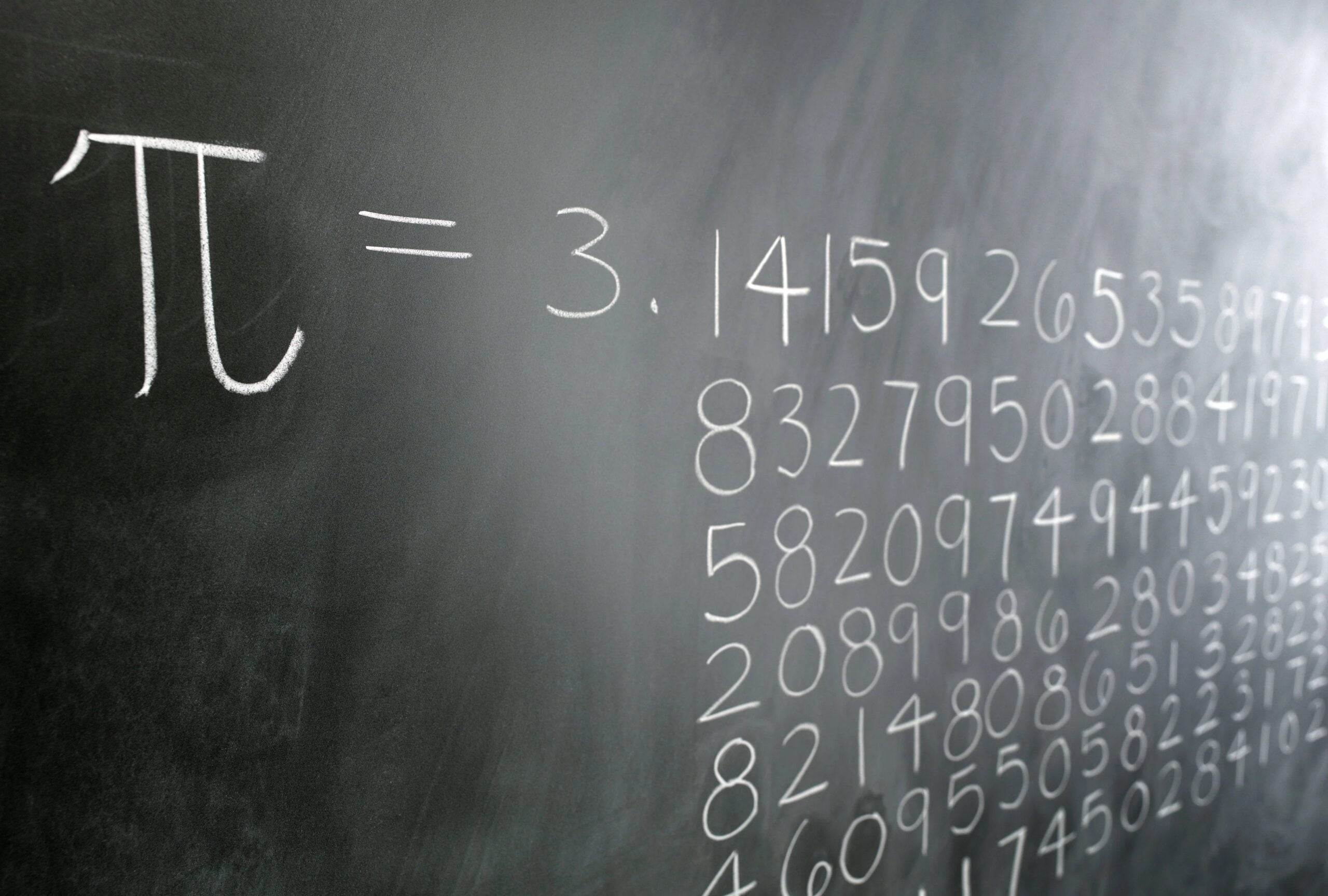গণিত
%22%20transform%3D%22translate(.5%20.5)%20scale(1.03516)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23dba100%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(28.24705%2038.31337%20-47.59955%2035.09342%2083.8%20144)%22%2F%3E%3Cellipse%20fill%3D%22%23a2dbff%22%20cx%3D%22169%22%20cy%3D%22255%22%20rx%3D%2271%22%20ry%3D%2276%22%2F%3E%3Cellipse%20fill%3D%22%239a5986%22%20cx%3D%2299%22%20cy%3D%22193%22%20rx%3D%2240%22%20ry%3D%2231%22%2F%3E%3Cellipse%20fill%3D%22%2397e7ff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(3.50025%20176.96539%20-20.86841%20.41276%20166.6%20104.3)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
গণিতের সৌন্দর্য্য পর্ব-৬: বিভ্রান্তিকর গড়
একধিক রাশির মধ্যে গড় নির্ণয়ের সবচেয়ে সহজ এবং বহুল ব্যবহৃত পদ্ধতিটি হলো মোট রাশির যোগফলকে মোট রাশির সংখ্যা দিয়ে ভাগ দেয়া। যেমন: পাঁচ জন ছাত্র যদি গণিতের একটি পরিক্ষায় ১০০ নম্বরের মধ্যে যথাক্রমে ৬৮, ৮২, ৭৫, ৯৩ এবং ৭৮ পেয়ে থাকে, তাহলে তাদের গণিতে প্রাপ্ত গড় নম্বর হবে ৭৯.২। ছাত্রদের মোট নম্বর ৩৯৬ কে মোট…
%27%20fill-opacity%3D%27.5%27%3E%3Cellipse%20fill%3D%22%23393939%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-768.68289%20-1.53466%20.17496%20-87.63517%20480.3%20765.5)%22%2F%3E%3Cellipse%20fill%3D%22%23f8f8f8%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(11.90836%20328.89048%20-995.44145%2036.04262%20458%20291.8)%22%2F%3E%3Cellipse%20fill%3D%22%23454545%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(5.62323%2056.33747%20-222.1033%2022.16886%20475.3%20815)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-51.75173%20-133.9208%20233.59591%20-90.26973%20680.2%202)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
গণিতের সৌন্দর্য্য: পর্ব-৪ (সবচেয়ে বড় সংখ্যাগুলো)
আজ কিছু বড় বড় সংখ্যা নিয়ে আলোচনা করব। আমাদের দৈনন্দিন জীবনে সবচেয়ে বড় যে সংখ্যাটি ব্যবহৃত হয় সেটা হল বিলিয়ন। টাকা গণনার জন্য এই সংখ্যাটি ব্যবহৃত হয়। আমাদের দেশের দু-চারজন মানুষ এই সংখ্যাটি ব্যবহার করেন। দেশের সামগ্রিক অর্থনীতির হিসাবের ক্ষেত্রে আরেকটু বড় সংখ্যা ব্যবহৃত হয়, ট্রিলিয়ন। এই ক্ষেত্রটির বাইরে আমাদের গণনা মিলিয়ন পর্যন্তই সীমাবদ্ধ। ১…
%27%20fill-opacity%3D%27.5%27%3E%3Cellipse%20fill%3D%22%23bb9671%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(177.9%2031.4%2028.8)%20scale(67.6959%20257.7604)%22%2F%3E%3Cpath%20fill%3D%22%23fff%22%20fill-opacity%3D%22.5%22%20d%3D%22M647%20277.6l-510%2071.5L287.1-37z%22%2F%3E%3Cellipse%20fill%3D%22%23fca964%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-67.02065%2028.12696%20-56.40581%20-134.40323%2022.9%201.2)%22%2F%3E%3Cellipse%20fill%3D%22%23c6d2da%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(123.6%20-35.3%20150.2)%20scale(208.74131%2074.63044)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
দ্বিপদী উপপাদ্য
আমার লেখার হাত অতটা ভালো না। তাই খুব একটা লিখি না। তবে এই বিষয়টা নিয়ে একটু লেখতে ইচ্ছা করল তাই শুরু করলাম। ঘটনার সুত্রপাত আমি যখন ইন্টারে উঠলাম তখন। আমাদের বইতে দ্বিপদী উপপাদ্য নামে একটা জিনিস(!!) পড়ানো হয় (কিংবা গলধকরন করানো হয়)। আগে সবাইকে মনে করিয়ে সেটা দেই। $$(a+b)^n=^{n}\textrm{C}_{0} a^n +^{n}\textrm{C}_{1}a^{n-1}b+\cdots \cdots+^{n}\textrm{C}_{r} a^n b^{n-r}+\cdots \cdots+^{n}\textrm{C}_{n}b^n$$…
%27%20fill-opacity%3D%27.5%27%3E%3Cpath%20fill-opacity%3D%22.5%22%20d%3D%22M85-155l-240%201930%201400-80z%22%2F%3E%3Cellipse%20fill%3D%22%23f1f1f1%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(-81.6%201496%20-1254)%20scale(726.79649%20641.10501)%22%2F%3E%3Cellipse%20fill%3D%22%23979797%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(390.30378%20674.42099%20-560.32698%20324.2748%201633.8%20581.6)%22%2F%3E%3Cellipse%20fill%3D%22%23232323%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-68.13145%20-2053.79657%20347.16774%20-11.51674%20258%20615)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
আজ π (পাই) দিবস এবং…
π (পাই) এর সাথে আমরা সবাই কমবেশি পরিচিত। যে কোনো বৃত্তের পরিধির দৈর্ঘ্য এবং ব্যাসের দৈর্ঘ্যের অনুপাত সর্বদা নির্দিষ্ট। এই নির্দিষ্ট অনুপাতটি π নামে পরিচিত। এর মান ৩.১৪১৫৯২৬৬৩……। π এর মানের সাথে মিলিয়ে প্রত্যেক বছর ৩য় মাসের ১৪ তারিখটিকে π দিবস, দুপুর ১টায় π ঘন্টা, ১ বেজে ৫৯ মিনিটে পাই মিনিট এবং ১ বেজে ৫৯…
%27%20fill-opacity%3D%27.5%27%3E%3Cellipse%20fill%3D%22%23fff%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-5.50577%20-450.63084%20362.02878%20-4.42324%20579%20229.6)%22%2F%3E%3Cellipse%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(1195.02406%20-26.25777%203.933%20178.99606%20768.5%20810)%22%2F%3E%3Cellipse%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(133.05291%203.43844%20-26.25015%201015.76946%201094.5%20546)%22%2F%3E%3Cellipse%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-135.45053%209.23409%20-65.33696%20-958.39712%2062%20409.9)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
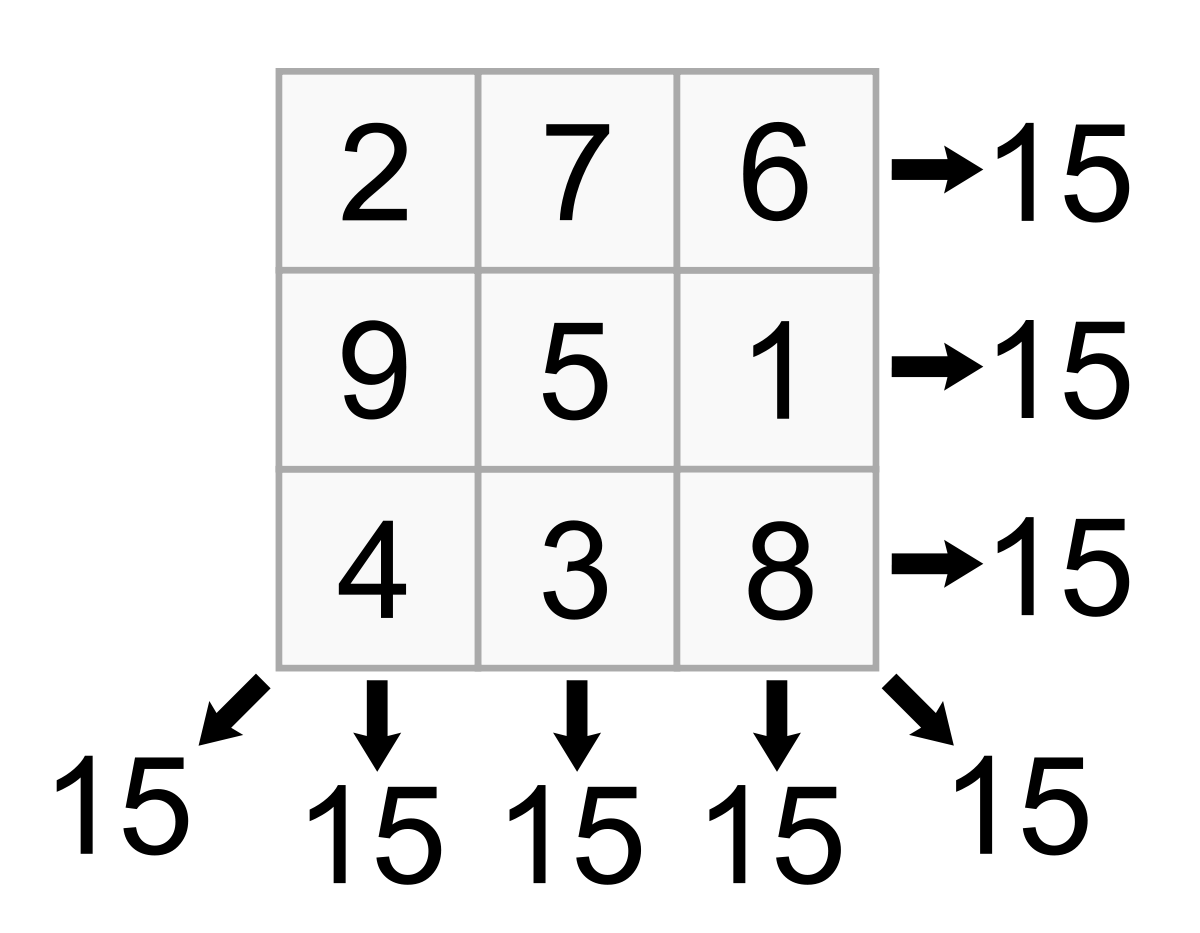
গণিতের সৌন্দর্য্য: পর্ব-৩ (ম্যাজিক স্কয়্যার)
ম্যাজিক স্কয়্যারের সাথে আমরা সবাই কমবেশি পরিচিত। ছোট বেলা থেকে সবাই নিশ্চয়ই ম্যাজিক স্কয়্যার দেখে এসেছেন এবং চমৎকারিতায় চমৎকৃত হয়েছেন। যারা এখনো বুঝতে পারেন নি তাদের জন্য বলছি ম্যাজিক স্কয়্যার হলো সমসংখ্যাক কলাম এবং সারি বিশিষ্ট সংখ্যার সজ্জা যেগুলোর সংখ্যাগুলোকে পাশা-পাশি, উপর-নিচ কিংবা কোণাকুনিভাবে যোগ করলে সর্বদা এই উত্তর পাওয়া যায়। ম্যাজিক স্কয়্যারের ইতিহাস যথেষ্ট…