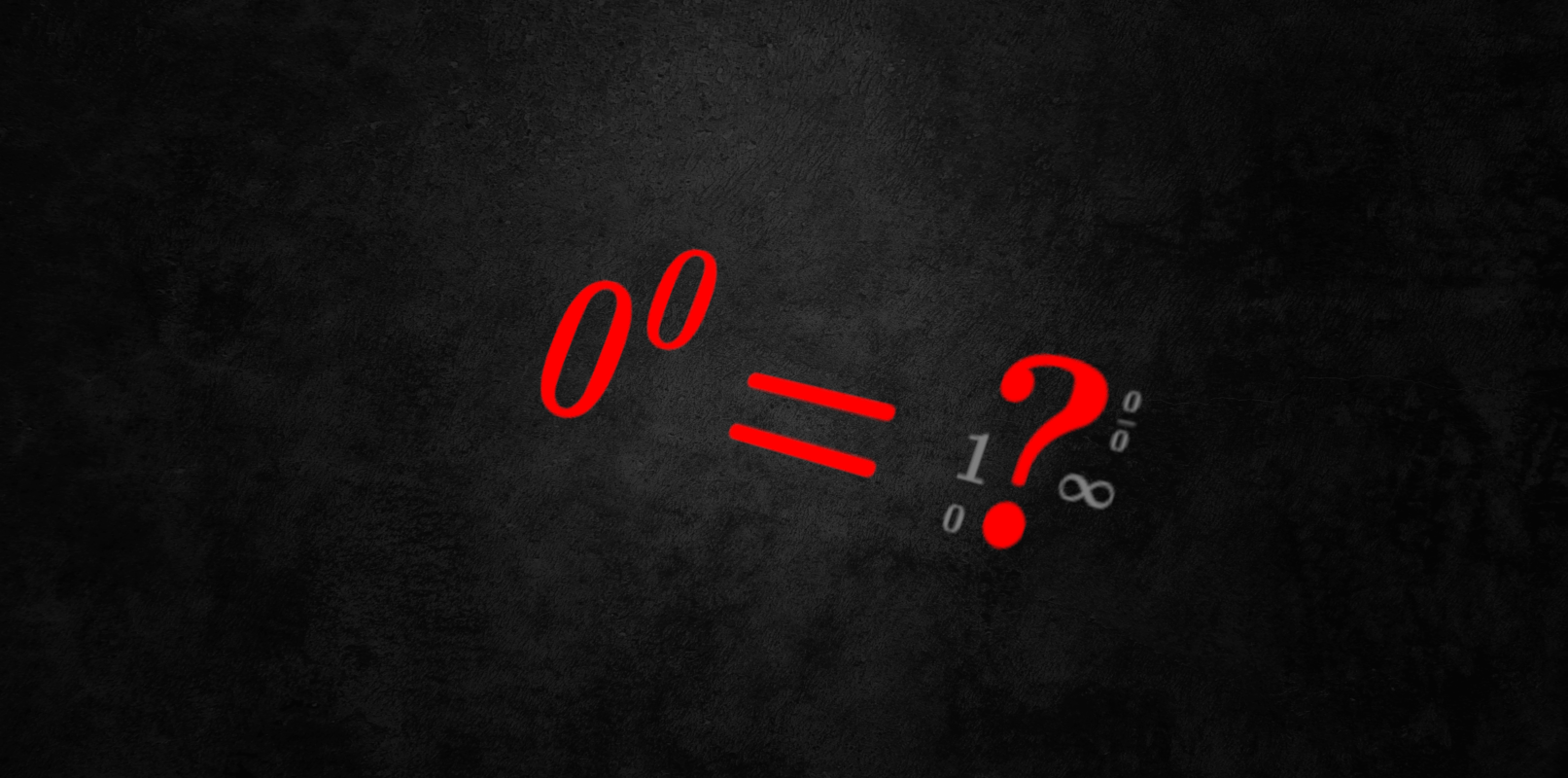গণিত
%22%20transform%3D%22matrix(5%200%200%205%202.5%202.5)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%238d8d8d%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-38.59041%2032.72705%20-27.92928%20-32.93307%2069%20100.7)%22%2F%3E%3Cellipse%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(5.11685%2041.96677%20-193.91574%2023.64343%2088.4%200)%22%2F%3E%3Cellipse%20fill%3D%22%23171717%22%20cx%3D%22201%22%20cy%3D%2290%22%20rx%3D%2267%22%20ry%3D%22255%22%2F%3E%3Cellipse%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(-9.3%20135.6%20-129.8)%20scale(98.7451%2022.10353)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
গণিতবিদ ময়ভার কি সত্যিই নিজের মৃত্যুদিবস ভবিষ্যদ্বাণী করেছিলেন?
আচ্ছা, তোমাকে যদি জিজ্ঞেস করা হয় যে, “বলো তো, তুমি কবে মৃত্যুবরণ করবে?” – উত্তরে তোমাদের মধ্যে কেউ কেউ হয়তো বলবে, “এটা আবার কি রকম বিচিত্র প্রশ্ন!” আবার, কেউ কেউ ধার্মিক হয়ে বলবে যে, “সৃষ্টিকর্তা ছাড়া কেউই মৃত্যুর দিন বলতে পারেনা, এমনকি ধারণাও করতে পারে না”। কিন্তু, এমন একজন ব্যক্তি ছিলেন যার সম্পর্কে প্রচলিত আছে…
%22%20transform%3D%22translate(.8%20.8)%20scale(1.5625)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23ffd6b6%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-41.26255%2043.68683%20-40.33856%20-38.10008%20124.1%2068.2)%22%2F%3E%3Cellipse%20fill%3D%22%234c1000%22%20cx%3D%22245%22%20cy%3D%2264%22%20rx%3D%2231%22%20ry%3D%22255%22%2F%3E%3Cpath%20fill%3D%22%23662c02%22%20d%3D%22M42-15.3l4%20231-88%201.6-4-231z%22%2F%3E%3Cellipse%20fill%3D%22%23cc9b36%22%20cx%3D%2248%22%20cy%3D%2269%22%20rx%3D%2228%22%20ry%3D%2247%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
মেটালিক রেশিও: গোল্ডেন রেশিওর মূল পরিবার
ড্যান ব্রাউনের দ্যা ভিঞ্চি কোড-এর কল্যাণে আমরা প্রায় সবাই গোল্ডেন রেশিও সম্বন্ধে জেনে গেছি। অনেক অনেক জায়গাতে এই গোল্ডেন রেশিও ব্যাবহার করা হয়, একে তো সৌন্দর্যের গাণিতিক মাপকাঠিও বলা হয়ে থাকে। কিন্তু গোল্ডেন রেশিওর মত সিলভার রেশিও সম্বন্ধে কি আমরা জানি? কিংবা এই গোল্ডেন রেশিও আর সিলভার রেশিও পরিবার মেটালিক রেশিও? কিভাবে বের করা যায়…
%22%20transform%3D%22translate(2.3%202.3)%20scale(4.5664)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23c6c6c6%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-32.91974%20-1.67476%201.3689%20-26.90757%202.2%204.7)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-.67002%2063.98012%20-135.4016%20-1.41797%20162.7%2033.6)%22%2F%3E%3Cpath%20fill%3D%22%23fff%22%20d%3D%22M271%2041L-16%2058l95-74z%22%2F%3E%3Cellipse%20fill%3D%22%23dfdfdf%22%20cx%3D%2222%22%20cy%3D%224%22%20rx%3D%2215%22%20ry%3D%2213%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
ফ্যাক্টোরিয়াল আর স্টার্লিং এর এপ্রক্সিমেশন
ধরা যাক, আপনার কাছে n টি আলাদা রঙের বল আছে। আপনি এদেরকে কতভাবে এক লাইনে সাজাতে পারেন? এই সহজ প্রশ্নটির উত্তর হলো n! যাকে আমরা পড়ি n ফ্যাক্টোরিয়াল। উদাহরণস্বরূপ, লাল (R), কালো (B), সাদা (W) এই তিন রঙের বল থাকলে আমরা RBW, RWB, BRW, BWR, RWB, RBW এই ছয় উপায়ে এদের এক লাইনে সাজাতে পারি।…
%22%20transform%3D%22translate(1.4%201.4)%20scale(2.77344)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23c5c5c5%22%20cx%3D%22112%22%20cy%3D%22131%22%20rx%3D%2233%22%20ry%3D%2223%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(173.79373%20-.8339%20.26248%2054.70291%20118.1%2055.3)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20cx%3D%22219%22%20cy%3D%2286%22%20rx%3D%2279%22%20ry%3D%22161%22%2F%3E%3Cpath%20fill%3D%22%23fff%22%20d%3D%22M0%200h81v140H0z%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
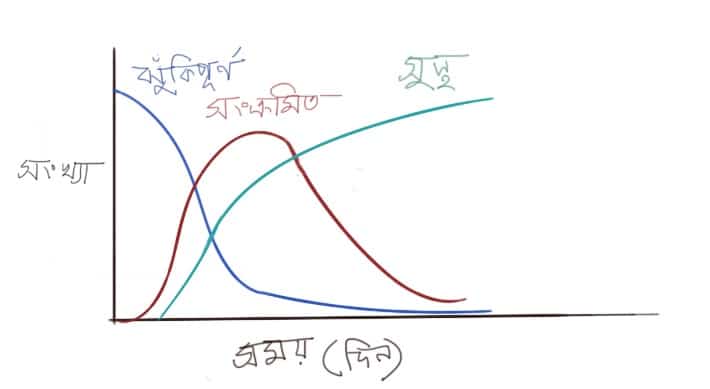
রোগতত্ত্ববিদ্যার গণিত যেভাবে মশা থেকে জন্ম নিলো
১. রোনাল্ড রস তখন ব্রিটিশ আর্মির সার্জন হিসেবে ভারতের ব্যাঙ্গালোরে কাজ শুরু করেছেন। সব মিলিয়ে খুশিই ছিলেন। ইংল্যান্ডের রয়েল কলেজ অব সার্জন থেকে বের হয়েছেন মাত্র বছর-দুই হলো। তরুণ বয়সে ইচ্ছা ছিলো লেখক হবেন; কিন্তু তার বাবা লন্ডনের একটি মেডিকেল কলেজে পড়াশুনার ব্যবস্থা করে দেন। রস যে মেডিকেল কলেজে কঠোর পরিশ্রমে পড়াশুনা করতেন এমন না।…
%22%20transform%3D%22translate(1.3%201.3)%20scale(2.69531)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23311900%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(5.23623%20-168.4697%2045.85194%201.42513%201.6%2059)%22%2F%3E%3Cellipse%20fill%3D%22%231b669d%22%20cx%3D%22118%22%20cy%3D%2216%22%20rx%3D%2218%22%20ry%3D%2238%22%2F%3E%3Cellipse%20fill%3D%22%23182900%22%20cx%3D%22228%22%20cy%3D%2210%22%20rx%3D%2231%22%20ry%3D%2229%22%2F%3E%3Cellipse%20fill%3D%22%23002f67%22%20cx%3D%22155%22%20cy%3D%22126%22%20rx%3D%22110%22%20ry%3D%22110%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
কন্ডিশনাল স্টেটমেন্ট এবং তার রকমভেদ
গণিতে প্রচুর পরিমাণে কন্ডিশনাল স্টেটমেন্ট ব্যবহৃত হয়, আমরাও আমাদের কথার মাঝে প্রচুর কন্ডিশনাল স্টেটমেন্ট ব্যবহার করি। যেমন, ‘যদি আজ বৃষ্টি নামে তবে বাংলাদেশ জিতে যাবে’, ‘যদি কোন আয়তের দুটি সন্নিহিত বাহু সমান হয় তবে এটি একটি বর্গ’। আমরা উদাহরণগুলো থেকে কন্ডিশনাল স্টেটমেন্টের কিছু বৈশিষ্ট্য খেয়াল করি- প্রতিটি স্টেটমেন্টের গঠন এরকম: ‘যদি Statement1 তবে Statement2’ (‘If…
%22%20transform%3D%22translate(1.6%201.6)%20scale(3.125)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%235f1f74%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(6.94645%2015.93339%20-26.13884%2011.3957%20127.3%20111.9)%22%2F%3E%3Cellipse%20fill%3D%22%23001747%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-12.769%203.75876%20-9.25267%20-31.43256%20110.8%2073.6)%22%2F%3E%3Cellipse%20fill%3D%22%23002753%22%20cx%3D%22106%22%20cy%3D%2259%22%20rx%3D%2217%22%20ry%3D%2217%22%2F%3E%3Cpath%20fill%3D%22%2346357a%22%20d%3D%22M101%20133l3-39%2040%2034z%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
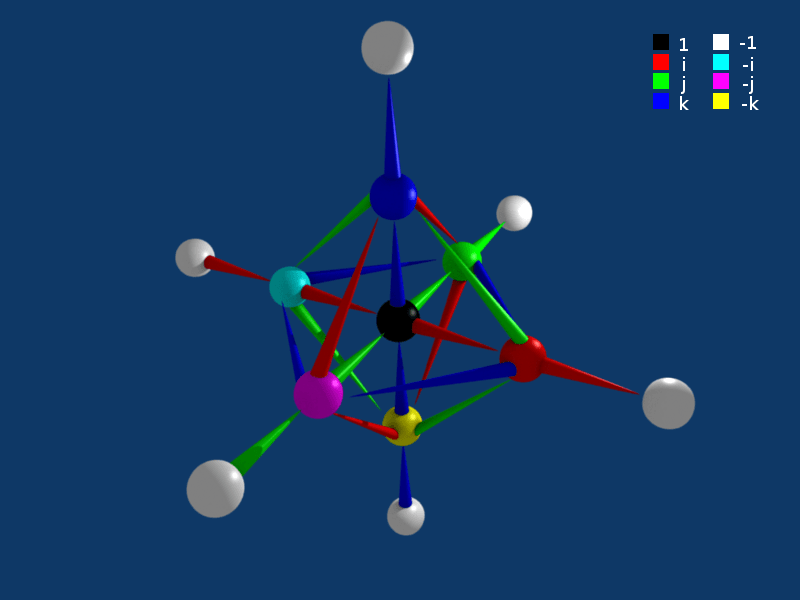
কোয়াটারনিয়ন: সংখ্যার এক অন্যভুবন
ঘড়ির ঘণ্টার কাটা ঘুরানোর কথা চিন্তা করুন। গণিতবিদেরা অনেক আগে থেকেই জানেন কিভাবে এধরনের ঘূর্ণনকে সাধারণ গুণন দিয়ে ব্যাখ্যা করা যায়। খুব সহজ, যে সংখ্যা দিয়ে কাটার অবস্থান প্রকাশ করা হল, সেটাকে আরেকটা ধ্রুবক সংখ্যা দিয়ে গুণ করলে ঘুরে যাবে অবস্থান। এ ঘুর্ণন তো ছিল একটা তলে, মানে দ্বিমাত্রিক ঘুর্ণন। তাহলে এরকম সহজ উপায় দিয়ে…
%22%20transform%3D%22translate(1.6%201.6)%20scale(3.125)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23fff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-254.02965%20-22.22471%202.21915%20-25.36505%20150.4%2014.6)%22%2F%3E%3Cellipse%20fill%3D%22%23d7d7d7%22%20cx%3D%22133%22%20cy%3D%2274%22%20rx%3D%2256%22%20ry%3D%2256%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-18.94668%20-20.06451%2065.03097%20-61.40797%2047.3%200)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-21.98897%2024.68376%20-103.62839%20-92.31498%20241.6%2040)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
অসীম ধারার গল্প
নবম দশম শ্রেণীতে আমাদের অসীম ধারার সাথে পরিচয় ঘটে। বিশেষ করে গুণোত্তর ধারার সাথে পরিচয় হওয়ার দিন কয়েক পরেই আমরা শিখি যে ,$$ \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdots \cdots = 1$$ সাধারণভাবে এটা আমরা গাণিতিকভাবে মেনে নেই, কিন্তু কেনো অসীম পর্যন্ত নিয়ে সমষ্টি $1$ পাওয়া যায়, তা বোঝার চেষ্টাও করি না।দেখা যাক আমরা…
%22%20transform%3D%22translate(3.2%203.2)%20scale(6.30078)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%232f2f2f%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-9.31827%20-88.00188%2069.72295%20-7.38277%20117.3%2041)%22%2F%3E%3Cellipse%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-21.74105%20206.52833%20-51.38098%20-5.40883%20235.2%2067.2)%22%2F%3E%3Cellipse%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(39.17133%20226.7778%20-31.20514%205.39006%2029.3%20117.3)%22%2F%3E%3Cellipse%20cx%3D%22221%22%20cy%3D%2262%22%20rx%3D%2235%22%20ry%3D%22255%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
0 এর 0 তম সূচক কত?
১৯ শতকের প্রথমদিকেও গণিতবিদদের মহলে শূন্যের শূন্যতম ঘাত বা সূচক $(0^0)$ এর ব্যাখ্যা একটি বিতর্কের বিষয় ছিল। সেসময়কার অধিকাংশ গণিতবিদেরা মেনে নিয়েছিলেন $0^0=1$। কিন্তু সমস্যা বেধেছিল, ১৮২১ সালে গণিতবিদ Cauchy $0^0$ কে $\frac{0}{0}$ এর মত অনির্ণেয় আকারগুলোর সাথে একই তালিকাভুক্ত করলেন। আবার ১৮৩০ এর দশকে গণিতবিদ Libri $0^0=1$ এর পক্ষে তার যুক্তি প্রকাশ করেছিলেন। সেটাও…
%22%20transform%3D%22matrix(6.25%200%200%206.25%203.1%203.1)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23070608%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(19.3866%2041.76484%20-58.66753%2027.23256%20106%20188)%22%2F%3E%3Cellipse%20fill%3D%22%23f9f8fa%22%20cy%3D%2280%22%20rx%3D%2236%22%20ry%3D%22203%22%2F%3E%3Cpath%20fill%3D%22%23e8eada%22%20d%3D%22M-14.1%2046.3l5.5-105.9%20254.7%2013.3-5.5%20105.9z%22%2F%3E%3Cellipse%20fill%3D%22%23dee1cf%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-8.14675%20-202.83646%2027.35735%20-1.09878%20202.9%20158)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
জীববিজ্ঞানে গণিতঃ মেন্ডেল ও মটরশুটি
আমাদের নৈসর্গিক এই মহাবিশ্বকে ব্যাখ্যা করার জন্য কিছু মৌলিক সূত্র রয়েছে, এই ধারনার সাথে আমরা সবাই অভ্যস্ত। আমরা নিজেরাই এই সূত্রগুলোর গাণিতিক প্রকাশ থেকে বিভিন্ন ঘটনা বা প্রকৃয়া যেমন একটা ফুটবলের গতিপথ, পারমাণবিক চুল্লীর চেইন রিঅ্যাকশন কিংবা মোবাইল ফোন থেকে টাওয়ারের সংকেতের আদান প্রদানে সিস্টেমের আচরনকে অনুমান করতে পারি। তবে জীববিজ্ঞানের ক্ষেত্রে এমনটা বলা কঠিন।…