গণিতের সৌন্দর্য্য: পর্ব-৩ (ম্যাজিক স্কয়্যার)

ম্যাজিক স্কয়্যারের সাথে আমরা সবাই কমবেশি পরিচিত। ছোট বেলা থেকে সবাই নিশ্চয়ই ম্যাজিক স্কয়্যার দেখে এসেছেন এবং চমৎকারিতায় চমৎকৃত হয়েছেন। যারা এখনো বুঝতে পারেন নি তাদের জন্য বলছি ম্যাজিক স্কয়্যার হলো সমসংখ্যাক কলাম এবং সারি বিশিষ্ট সংখ্যার সজ্জা যেগুলোর সংখ্যাগুলোকে পাশা-পাশি, উপর-নিচ কিংবা কোণাকুনিভাবে যোগ করলে সর্বদা এই উত্তর পাওয়া যায়।

ম্যাজিক স্কয়্যারের ইতিহাস যথেষ্ট প্রাচীন। খ্রীষ্টপূর্ব ৬৫০ সালে চীনে ম্যাজিক স্কয়্যারের প্রচলন ছিল। এরপর ৭ম খ্রীস্টাব্দের আরবীয় কিছু নমুনায় ম্যাজিক স্কয়্যারের খোঁজ পাওয়া যায়। এছাড়াও অনেক প্রাচীন সভ্যতার ধ্বংসাবশেষে ম্যাজিক স্কয়্যার খুঁজে পাওয়া গেছে। প্রাচীন কাল থেকে ম্যাজিক স্কয়্যারের অদ্ভুত প্যাটার্ন দেখে মানুষ অভিভূত হয়েছে। একসময় এটাকে সত্যিই জাদুকরী মনে করা হত। বিভিন্ন রকম প্রাচীন তাবিজ-কবোজে এর ব্যাবহার খুঁজে পাওয়া গেছে। জ্যোতিষ শাস্ত্রেও এর ব্যবহার লক্ষ করা যায়। ষষ্ঠদশ শতকে ইউরোপের জ্যোতিষশাস্ত্রে ম্যাজিক স্কয়ারের উল্লেখযোগ্য ব্যবহার দেখা যায়। সৌরজগতের বিভিন্ন গ্রহকে বিভিন্ন মাত্রার ম্যাজিক স্কয়্যার দিয়ে সংখ্যায়িত করা হয়।

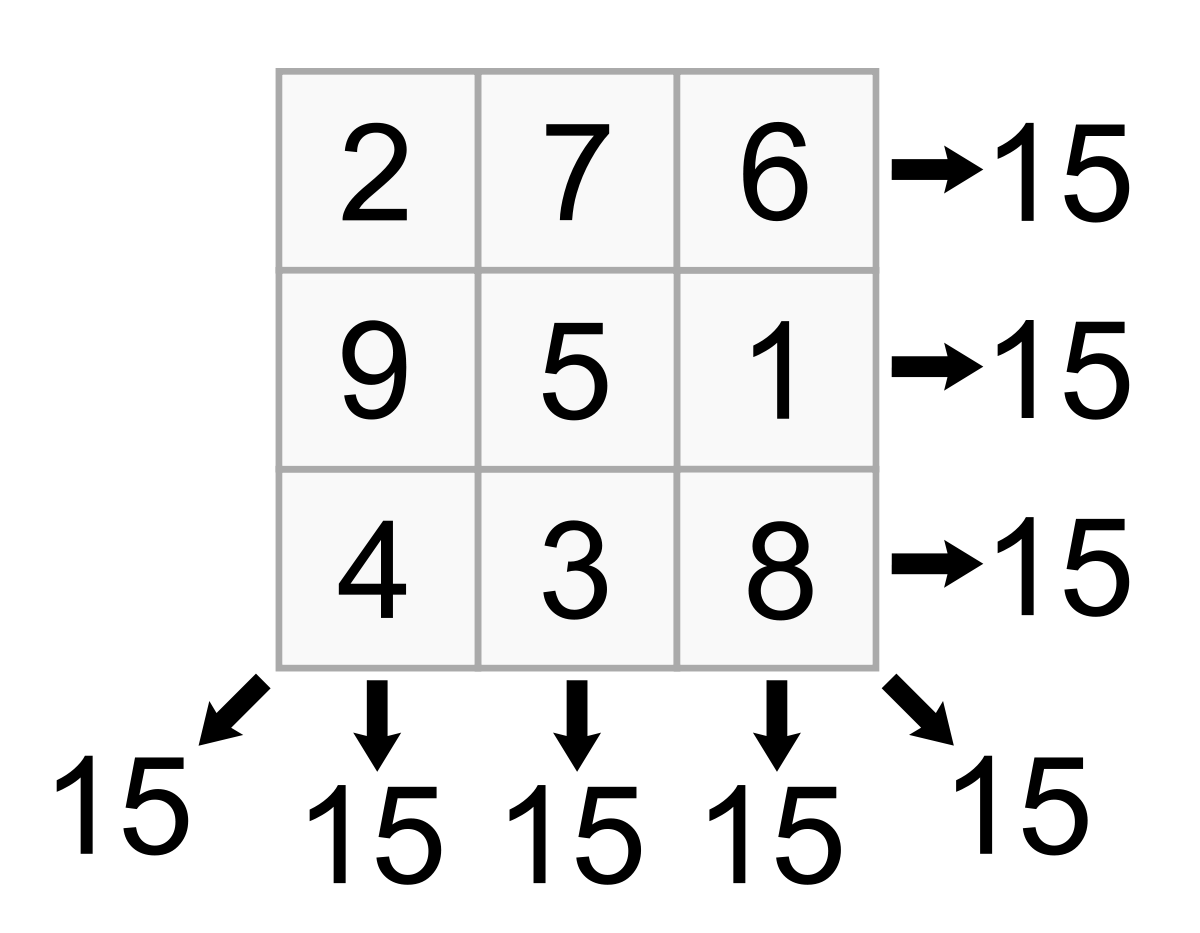
এবার নিচের ম্যাজিক স্কয়্যারটি দেখুন:

উপরে-নিচে, ডানে-বাঁয়ে কোণাকুনি যোকোন দিকেই যোগ করলে যোগফল হবে ১৫। ১৫ হল এই স্কয়ারটির ম্যাজিক কনস্ট্যান্ট। এরচেয়ে একটু বড় দেখতে চাইলে নিচের ৫X৫ স্কয়্যারটি দেখতে পারেন:

এই স্কয়্যারটির ম্যাজিক কন্সট্যান্ট হল ৬৫। একটু দৈর্য্য ধরলে অনেক বড় ম্যাজিক স্কয়্যার আঁকা সম্ভব। যেমন:

 এতবড় স্কয়্যার দেখে চমকে যাওয়ার কিছু নেই। এটা আসলে অনেকগুলো ৩X৩ স্কয়ার জোড়া দিয়ে বানানো হয়েছে!

তবে ম্যাজিক স্কয়্যার যতই ম্যাজিকাল মনে হোক, এগুলো বেশ সহজ কিছু পদ্ধতিতে আঁকা যায়। আপনি চাইলে খুব সহজেই উপরের বড় স্কয়্যারটির মত বড়-সড় স্কয়্যার বানিয়ে ফেলতে পারেন। একটি পদ্ধতি এরই মধ্যে জেনে গেছেন। সেটা হলো ছোটো-ছোটো স্কয়্যার জোড়া দেয়া। তবে জোড়া না দিয়েও অনেক বড় বড় ম্যাজিক স্কয়ার তৈরি করে ফেলতে পারবেন। ম্যাজিক স্কয়্যার বানানোর কিছু পদ্ধতি এখানে আলোচনা করব।

পদ্ধতি এক:
এই পদ্ধতিতে যেকোন আকৃতির বিজোড় মাত্রার ম্যাজিক স্কয়্যার আকতে পারবেন। উদাহরন হিসেবে একটি ৫X৫ মাত্রার বর্গ নেয়া যাক। এবার এর মাঝের কলামের একেবারে উপরে একটি সংখ্যা লিখুন ইচ্ছামত। আমি ১ থেকে শুরু করলাম।

এবার এই কলামের ডানপাশে একেবারে নিচে পরের সংখ্যাটি লিখুন। অর্থাৎ আমার এই ক্ষেত্রে লিখতে হবে ২।

আসলে নিয়মটি হল যখনই একটি সংখ্যা লিখবেন তার পরের সংখ্যাটি লিখতে হবে ডানদিকের উপরের কোনাকুনি বরাবর। কিন্তু এক লেখার পর যেহেতু ডানদিকে উপরে যাওয়া যাচ্ছে না তাই একেবারে নিচে নেমে যেতে হবে। তাহলে পরের সংখ্যাটি লিখতে হবে এভাবে:

যখন দেখবেন কোণাকুনি যেতে যেতে একেবারে ডানে চলে এসেছেন তখন একসারি উপরে উঠে একেবারে বামদিকের কলামে চলে আসবেন। অর্থাৎ ৪ লিখতে হবে ৩ এর একসারি উপরে একেবারে বাম দিকে।

এই পর্যন্ত আশা করি বুঝতে পেরেছেন। এবার আগের নিয়মে কোণাকুনি উপরে উঠতে থাকুন। যদি কোনো সংখ্যা দ্বারা বাধাপ্রাপ্ত হন তাহলে একঘর নেমে আবার কোণাকুনি উপরে উঠতে থাকুন।একেবারে উপরে উঠে গেলে একঘর ডানে একেবারে নিচে নেমে আসুন (১ থেকে যেভাবে ২ এ এসেছিলেন)। এবং একই নিয়মে চালিয়ে যান।

১৫ পর্যন্ত লেখার পর দেখবেন একেবারে উপরে ডানদিকের কোনায় চলে এসেছেন। কিন্তু নিয়মানুযায়ী ডানের নিচেও যাওয়া যাচ্ছে না আবার উপরের বামেও যাওয়া যাচ্ছে না। এই ক্ষেত্রেও একঘর নেমে আবার একই নিয়মে রওনা দিন।

শেষ হয়ে গেলে এবার সবদিক থেকে যোগ করে মিলিয়ে দেখুন।

পদ্ধতি দুই: উপরের পদ্ধতিতে বিজোড় মাত্রার ম্যাজিক স্কয়্যার করা গেলেও জোড় মাত্রার জন্য নিচের পদ্ধতি অবলম্বন করতে হবে।

যেকোন জোড় মাত্রার বর্গ সংখ্যা নিন। এবার প্রথম থেকে শেষ ঘর পর্যন্ত পর্যায়ক্রমে সংখ্যাগুলো লিখে চিন্হিত করুন।

এবার কোণাকুনি সংখ্যাগুলো রেখে বাকিগুলো মুছে ফেলুন। অর্থাৎ ১,৪,৬,৭,১০,১১,১৩,১৬ সংখ্যাগুলো থাকবে। বাকিগুলো মুছে যাবে।

এবার যেই ক্রমে ১ থেকে ১৬ লিখেছিলেন তার বিপরীতক্রমে লিখে খালিঘরগুলো পূরণ করে ফেলুন।

এই বিপরীত ক্রম থেকে অবশিষ্ট সংখ্যাগুলো লিখুন।

আপনি আপনার ইচ্ছামত সংখ্যা বাছাই করে শুরু করতে পারেন। আমি যদিও ১ থেকে শুরু করেছি, আপনি চাইলে ১৫, ৩৭ বা ১০০ থেকেও শুরু করতে পারেন। আবার পরপর সংখ্যা না নিয়ে ২টি, ৩টি বা ৪টি বাদ দিয়েও নিতে পারেন।

এবার কিছু অনিন্দ্য সুন্দর ম্যাজিক স্কয়্যার:

১.

এই ম্যাজিক স্কয়্যারটি উদ্ভাবন করেছিলেন চিত্রশিল্পী অ্যালব্রেখট ডুরার। তিনি একজন গণিতবিদও ছিলেন। মেলানকোলিয়া আই নামক ছবিতে তিনি এই স্কয়ারটি দেখিয়েছেন। এটির বিশেষত্ব হল, শুধু পাশা-পাশি, উপর-নীচ বা কোণাকুনি নয়, এর পাশাপাশি চারঘর নিয়ে একটি ২X২ মাত্রার বর্গের চারটি সংখ্যার যোগফলও একই হয়!

২. প্রাইম ম্যাজিক:

এই ম্যাজিক স্কয়্যারটির প্রত্যেকটি সংখ্যা প্রাইম।

৩. বেন্জামিন ফ্রাংকলিন নিচের ম্যাজিক স্কয়্যারটি উদ্ভাবন করেন:

এর বিশেষত্ব হল:
ক. এর যেকোন কলাম বা যেকোন সারির ১৬ টি সংখ্যার যোগফল ২০৫৬ এবং এই স্কয়ারটির যেকোন ৪X৪ নিয়ে যে ১৬ সংখ্যার বর্গ পাওয়া যায়, তাদের যোগফলও ২০৫৬!!!
খ. এটিকে নিচের প্যাটার্নগুলোর মত করে যোগ করলেও যোগফল হয় ২০৫৬। (একই রং বিশিষ্ট ঘরের সংখ্যাগুলোকে একসাথে যোগ করতে হবে)।

৪. জটিল(complex) সংখ্যার ম্যাজিক স্কয়্যার:

আজ বিদায় নেয়া যাক। সবাইকে আগামী পর্ব দেখার অগ্রীম আমন্ত্রন জানাই।