নিচের লেখাটিকে cryptic note হিসেবে ধরা যেতে পারে। সময়ের সাথে সাথে এর পরিমার্জনা ও পরিবর্ধন হবে।
[১] ১৯২৩ সনে, ফরাসী পদার্থবিদ দ্যব্রগলি আইনস্টাইনের বিশেষ আপেক্ষিকতা তত্ত্ব ও প্লাঙ্কের কোয়ান্টাম তত্ত্ব মিলিয়ে আলো কোয়ান্টার একটা নতুন পরীক্ষামূলক বা সাময়িক তত্ত্ব দিলেন। দ্য ব্রগলির নাম ইংরেজীতে লেখা হয় Luis de Broglie। এর ইংরেজী উচ্চারণ লুই দ্যব্রলি’র মতন আর ফরাসী হচ্ছে লুই দ্যব্রইয়ে’র মতন, আমরা বাংলায় এত দিন যেমন প্রচলিত সেটাই রাখছি, দ্যব্রলি বা দ্যব্রইয়ে বলে বলে পাঠককে ঘাবড়ে দিচ্ছি না।
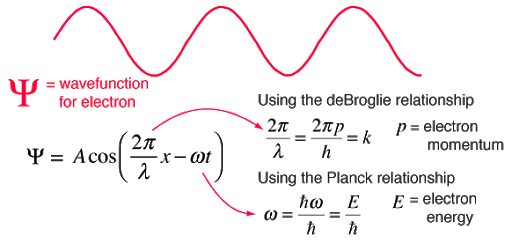
আলো-কোয়ান্টামের শক্তিকে প্লাঙ্ক বর্ণনা করেছিলেন $E=h\nu$ হিসেবে, আর আইনস্টাইনের তত্ত্ব থেকে পাওয়া গেল $E=pc$। এখানে $h$ হচ্ছে প্লাঙ্কের ধ্রুবক, $p$ ভরবেগ, $c$ হল আলোর গতিবেগ এবং $\nu$ হচ্ছে কোন তরঙ্গের কম্পাঙ্ক। অন্যদিকে $\nu = \frac{c}{\lambda}$ যেখানে $\lambda$ হল সেই তরঙ্গের তরঙ্গদৈর্ঘ্য। কাজেই $\lambda = \frac{c}{v} = \frac{h}{p}$ এটাকেই দ্যব্রগলির সম্পর্ক বা নীতি বলা হয়।
দ্যব্রগলি আরো বললেন এই সম্পর্ক যে কোন রৈখিক ভরবেগ $p$ সম্পন্ন গতিশীল কণার ক্ষেত্রে খাটবে। আর তাই যে কোন চলন্ত কণার তরঙ্গ বৈশিষ্ট থাকবে। এর ওপর ভিত্তি করে তাঁর একটি ভাবীকথন ছিল – একটি ইলেকট্রনের রশ্মিকে ডিফ্রাকশান (অপবর্তন) করানো যাবে।

[২] সহজ কথায় অপবর্তন হচ্ছে কোন তরঙ্গ বাধাগ্রস্থ হলে সেই তরঙ্গ বেঁকে যাবে। দ্যব্রগলি বললেন আলোর মত ইলেকট্রনকে একটি সরু ফাটলের মধ্য দিয়ে পাঠালে তার বিচ্ছুরণ হবে। ১৯২৫ সনে ডাভিসন ও গেরমার বড় নিকেলের কেলাসের মাঝে ইলেকট্রনের অপবর্তন অবলোকন করলেন। সেই বছরই টমসন ও রিড ইলেকট্রন রশ্মিকে পাতলা সোনার মধ্যে দিয়ে অতিক্রম করিয়ে তার অপবর্তন দেখলেন। কণারও যে তরঙ্গ বৈশি আছে সেটা প্রমাণ হল।
১৯২৫ সালের নভেমবর মাসেই অস্ট্রিয়ান বিজ্ঞানী আরউইন শ্রোডিঞ্জার জুরিখে দ্যব্রগলির অনুকল্পের ওপর একটি সেমিনার দেন, সেই সেমিনারে ওলন্দাজ বিজ্ঞানী পিটার দিবাই (হয়তো উচ্চারণ হবে দিবে) উপস্থিত ছিলেন। দিবাই নাকি সেখানে মন্তব্য করেছিলেন, ইলেকট্রন যদি তরঙ্গই হয় তবে তার জন্য একটা তরঙ্গ সমীকরণ সৃষ্টি করতে হবে।

[৩] ডিসেম্বর মাসে, বড়দিনের ছুটিতে শ্রোডিঞ্জার গেলেন আলপস পাহাড়ে। সাথে নিলেন না তাঁর স্ত্রীকে, নিলেন তাঁর পুরাতন বান্ধবীকে। বিরাট স্ক্যান্ডাল। ইতিহাসে সেই বান্ধবীর পরিচয় জানা যায় না, কিন্তু শ্রোডিঞ্জারকে তরঙ্গ সমীকরণ উদ্ভাবন করাতে তাঁর অবদান আছে এটা সবাই বলেন। আলপসের ছুটি শেষে শ্রোডিঞ্জার তাঁর সমীকরণটি নিয়ে জুরিখ ফিরলেন।
[৪] এই সমীকরণটিকে আহরণ করার একটা সহজ পদ্ধতি শ্রোডিঞ্জার দিয়ে গেছেন। তিনি শুরু করেছিলেন ধ্রুপদী তরঙ্গ সমীকরণ দিয়ে যা কিনা স্থান (দেশ) ও সময়ের সাথে যে কোন তরঙ্গের পরিবর্তনকে বর্ণনা করে। তাই ধ্রুপদী সমীকরণকে আবার দুটো ভাগে ভাগ করা যাবে। একটি ভাগ হচ্ছে শুধুমাত্র স্থান বা দেশ নির্ভর। অন্যটি সময় নির্ভর। শুধুমাত্র স্থান-নির্ভর ধ্রুপদী তরঙ্গ সমীকরণকে এই ভাবে লেখা যেতে পারে – $$\begin{align} \nabla^2 \psi = – k^2 \psi \label{১} \tag{১} \end{align} $$ এখানে $\nabla^2$ কে বলা হয় লাপ্লাসিয়ান অপরেটর। কার্তেশিয়ান স্থানাংক ব্যবস্থায়, $$\nabla^2 = \frac{\partial^2}{\partial x^2}+ \frac{\partial^2}{\partial y^2}+ \frac{\partial^2}{\partial z^2}$$
$k =\frac{2\pi}{\lambda}$ হচ্ছে তরঙ্গ ভেক্টর যেখানে $\lambda$ হল তরঙ্গদৈর্ঘ্য। $\eqref{১}$ নম্বর সমীকরণটির অনেক ধরণের সমাধান সম্ভব, অর্থাৎ $\psi$ তরঙ্গ ফাংশান নানাবিধ রূপ নিতে পারে, সাইন ও কোসাইন ফাংশান থেকে আরম্ভ করে বহু জটিল ধরণের ফাংশান এই সমীকরণের উত্তর হতে পারে।
আমরা আগেই দেখেছি দ্যব্রগলির ধারণা অনুযায়ী $\lambda = \frac{h}{p}$, যেখানে $p$ হল তরঙ্গ-কণার রৈখিক ভরবেগ। আমরা যদি অনাপেক্ষিক তত্ত্ব অনুযায়ী ধরে নিই $p = mv$ যেখানে $m$ হচ্ছে কণার ভর। কাজেই $$ k =\frac{2\pi}{\lambda} = \frac{2\pi p}{h} = \frac{2\pi mv}{h} $$ তাহলে $$\begin{align} \nabla^2 \psi = – \frac{4\pi^2 m^2 v^2}{h^2} \psi \label{২} \tag{২} \end{align} $$ কণাটির পুরো শক্তির পরিমাণ $(E)$ হল তার গতিশক্তি ও স্থিতিশক্তির $(V)$ সমষ্টি। $$E = \frac{1}{2}mv^2 + V$$ দেখাই যাচ্ছে ওপরের সমীকরণটি আমরা এইভাবে লিখতে পারি $$mv^2 = 2(E-V)$$ আর এটাকে $\eqref{২}$ নম্বর সমীকরণে প্রতিস্থাপিত করলে আমরা পাব, $$ \begin{align} \nabla^2 \psi & = – \frac{8\pi^2 m}{h^2}(E-V) \psi \\ \implies -\frac{\hbar^2}{2m} & \nabla^2 \psi + V\psi = E \psi \label{৩} \tag{৩} \end{align} $$ এখানে $\hbar = \frac{h}{2\pi}$; এই $\hbar$ কে এইচ-বার উচ্চারণ করা হয়।
$\eqref{৩}$ নম্বর সমীকরণকে শ্রোডিঞ্জারের সময়-নিরপেক্ষ ত্রিমাত্রিক সমীকরণ বলা হয়। শ্রোডিঞ্জারের আদি ডিরাইভেশন অনেকটা এরকমই ছিল, ধ্রুপদী তরঙ্গ সমীকরণে তরঙ্গদৈর্ঘ্যকে দ্যব্রগলি অনুকল্প অনুযায়ী বদলে দেওয়া। এর পরে বহুজন বহুভাবে এই সমীকরণ ডিরাইভ করেছেন, শ্রোডিঞ্জার নিজেও তার আবিষ্কার একটু ভিন্নভাবে উপস্থাপনা করেছিলেন। কিন্তু এর মূলে তরঙ্গকে তরঙ্গ-কণা হিসেবে দেখার বিবেচনাটা প্রাধান্য পেয়েছিল।







Leave a Reply to আরাফাত রহমানCancel reply