সুপ্রাচীন কাল থেকেই বিভিন্ন সাজসজ্জায় এবং স্থাপত্যে বিভিন্ন রকমের নকশার ব্যাবহার দেখা যায় । দেয়াল কিংবা মেঝের কারুকার্যে দ্বিমাত্রিক ভাবে বিন্যস্ত নকশা অথবা ছাদের কিনারা বা বিভিন্ন পাত্রে ফালির মতো একমাত্রিক ভাবে বিন্যস্ত নকশা দেখা যায়। এই নকশা সমূহ সাধারণত বিশেষ প্রতিসাম্য বিশিষ্ট হয়ে থাকে যারা একটা নির্দিষ্ট আকারকে পুনরাবৃত্তির মাধ্যমে তৈরি হয়ে থাকে যাকে বলা হয় মোটিফ। মোটিফ গুলো পুনরাবৃত্তি করে থাকে প্রতিসাম্য রূপান্তরের মাধ্যমে প্রতিসম ভাবে বিন্যস্ত সকল মোটিফ একটা মোটিফের উপর বিভিন্ন প্রতিসাম্য রূপান্তর দ্বারা প্রতিলিপি তৈরির মাধ্যমে তৈরি হয়ে থাকে। একটা একমাত্রিক ভাবে বিন্যস্ত নকশায় শুধু সাত রকমের প্রতিসাম্য পাওয়া যায় ফালি বা ফিতার মতো এই নকশা সমূহকে বলা হয় ফ্রেজ প্যাটার্ন । গণিতবিদ জন কনওয়ে পদচিহ্ন অনুযায়ী এই সাত রকমের ফ্রেজনকশার নামকরণ করেন ।

নিচের চিত্রের সাতটি নকশার প্রথমটিতে একটা মোটিফকে পর্যায়ক্রমিক ভাবে নির্দিষ্ট দূরত্বে স্থানান্তর করে উৎপন্ন হয়েছে তাই এই নকশায় শুধু স্থানান্তর প্রতিসাম্যতা রয়েছে কনওয়ে একে বলেন হপ্ বা খোঁড়ানো। দ্বিতীয় নকশা মোটিফের উপর স্থানান্তর এবং প্রতিফলন পর্যায়ক্রমিকভাবে প্রয়োগে উৎপন্ন হয়েছে প্রথমে মোটিফকে স্থানান্তর এবং পরে অনুভূমিক রেখায় প্রতিফলিত রূপ নিতে হবে এভাবে যে রূপান্তর হয় তাকে বলা হয় গ্লাইড রিফ্লেকশন কনওয়ে একে বলেন স্টেপ বা হেটে যাওয়া। তৃতীয়টায় ১৮০ ডিগ্রীতে ঘূর্ণন এবং স্থানান্তর পর্যায়ক্রমিক প্রয়োগের মাধ্যমে উৎপন্ন হয়েছে মোটিফকে প্রথমে ১৮০ ডিগ্রীতে ঘুড়িয়ে পরে স্থানান্তর করে আবার ঘুড়িয়ে। এটার স্থানান্তর এবং ঘূর্ণন প্রতিসাম্যতা রয়েছে একে বলা যায় ডিযেইহপ বা ঘুরে ঘুরে খোঁড়ানো। চতুর্থ নকশা তৈরি হয় পর্যায়ক্রমিকভাবে উলম্বরেখায় প্রতিফলন রূপান্তর প্রয়োগ করে। ১ম মোটিফ উলম্ব রেখায় প্রতিফলন করে ২য়,২য়টা একিভাবে ৩য় এভাবে। কনওয়ের মতে একে বলা যায় সাইডল বা পাশেরদিকে হাটা। এটার স্থানান্তর এবং প্রতিফলন প্রতিসাম্যতা রয়েছে ।
 পঞ্চম নকশা প্রথমে অনুভূমিক রেখায় প্রতিফলন এবং তারপর স্থানান্তরের মাধ্যমে মোটিফকে পুনরাবৃত্তি করে তৈরি হয়েছে। এ ধরনের পায়ের ছাপ তৈরি করতে হলে লাফিয়ে চলতে হবে তাই এটার নাম জাম্প বা লম্ফ। ষষ্ঠ নকশায় স্থানান্তর,গ্লাইড রিফ্লেকশন এবং ঘূর্ণন তিন রকমের প্রতিসাম্যতা রয়েছে অর্থাৎ একটা মোটিফের উপর তিন রকমের প্রতিসাম্য রূপান্তর প্রয়োগ করায়ায়। একে বলা যায় ঘুরতে ঘুরতে পাশেরদিকে হাটা। সপ্তম নকশায় চার রকমের প্রতিসাম্যতা রয়েছে(স্থানান্তর, উলম্ব ও অনুভূমিক রেখায় প্রতিফলন এবং ঘূর্ণন)এটার মোটিফে চার রকম প্রতিসাম্য রূপান্তর প্রয়োগ করায়ায় এবং একে বলা যায় ঘুরতে ঘুরতে লাফানো। একটা নির্দিষ্ট রূপান্তর পর্যায়ক্রমে হয়ে থাকে যার কারণে নকশা গুলো পর্যায়ক্রমিক নকশা। ফ্রেজপ্যাটার্ন সমূহ শুধু একটা রেখা বরাবর পুনরাবৃত্তি হয়ে থাকে তাই এগুলোকে বলা যায় একমাত্রিক নকশা কিন্তু দেয়ালের অথবা মেঝের কারুকার্যে যে নকশা সমূহ দেখা যায় সেগুলি দুই মাত্রিক ভাবে বিস্তৃত থাকে অর্থাৎ একটা মোটিফ দ্বিমাত্রিক তলে প্রতিসাম্য রূপান্তরের মাধ্যমে পুনরাবৃত্তি করে থাকে দ্বিমাত্রিক পর্যায়ক্রমিক নকশা রয়েছে ১৭ রকমের। এই দ্বিমাত্রিক নকশা সমূহে স্থানান্তর প্রতিসাম্যতা, ঘূর্ণন প্রতিসামতা (১৮০ ডিগ্রীতে, ১২০ ডিগ্রীতে, ৯০ডিগ্রীতে, এবং ৬০ডিগ্রীতে),গ্লাইডরিফ্লেকশন, উলম্ব ও অনুভূমিক রেখায় প্রতিফলন প্রতিসাম্যতা দেখাযায় এটা গাণিতিক ভাবে প্রমাণিত যে কোন পর্যায়ক্রমিক নকশা শুধু ১৮০ডিগ্রীতে, ১২০ডিগ্রীতে, ৯০ডিগ্রীতে, এবং ৬০ ডিগ্রীতে ঘূর্ণন রূপান্তরের মাধ্যমেই সম্ভব এদের বলা হয় ২ফোল্ড, ৩ফোল্ড, ৪ফোল্ড এবং ৬ফোল্ড ঘূর্ণন অক্ষ প্রতিসাম্য(n ফোল্ড=৩৬০/n)। ঘূর্ণন প্রতিসাম্যতা মানে যে পরিমাণ ঘুরালে কোন আকারকে একই রকম দেখায়। ১ফোল্ড প্রতিসাম্যতা আসলে কোন প্রতিসাম্যতা নয় কারণ একটা আকার যত অপ্রতিসমই হোক না কেন তা ৩৬০ ডিগ্রীতে ঘুরালে একইরকম দেখাবে। পর্যায়ক্রমিক নকশার বৈশিষ্ট্য হচ্ছে এরা একটা একক কোষ বা ইউনিট সেল পুনরাবৃত্তির মাধ্যমে গঠিত হয়ে থাকে ১৭ রকমের নকশায় মাত্র পাঁচ রকমের ইউনিট সেল দেখাযায়।কোন নকশায় মোটিফ গুলো সরিয়ে নিলে শুধু ইউনিট সেলের যে জাল পাওয়া যাবে তাকে বলে ল্যাটিস । ইউনিট সেলের শীর্ষবিন্দু(vertex) সমূহের বিন্যাসটা হচ্ছে ল্যাটিস আর শীর্ষবিন্দুগুলো হল ল্যাটিস বিন্দু। সতের রকমের নকশা পাঁচ রকম ল্যাটিস গঠন বিশিষ্ট হয়ে থাকে কোন নকশায় ৯০ ডিগ্রী ঘূর্ণন প্রতিসাম্যতা থাকলে তার ল্যাটিস অবশ্যই বর্গাকার হবে আবার যদি ৬০ ডিগ্রী ও ১৮০ডিগ্রী প্রতিসাম্যতা থাকে তাহলে ষড়ভুজাকার এবং উলম্ব রেখা প্রতিফলন প্রতিসম বিশিষ্ট নকশা সাধারণত আয়তাকার ল্যাটিস গঠন বিশিষ্ট হয়ে থাকে। নীচের চিত্রে সতের দ্বিমাত্রিক নকশা এবং তাদের একককোষ ও প্রতিসাম্যতা দেখানো হলো।
পঞ্চম নকশা প্রথমে অনুভূমিক রেখায় প্রতিফলন এবং তারপর স্থানান্তরের মাধ্যমে মোটিফকে পুনরাবৃত্তি করে তৈরি হয়েছে। এ ধরনের পায়ের ছাপ তৈরি করতে হলে লাফিয়ে চলতে হবে তাই এটার নাম জাম্প বা লম্ফ। ষষ্ঠ নকশায় স্থানান্তর,গ্লাইড রিফ্লেকশন এবং ঘূর্ণন তিন রকমের প্রতিসাম্যতা রয়েছে অর্থাৎ একটা মোটিফের উপর তিন রকমের প্রতিসাম্য রূপান্তর প্রয়োগ করায়ায়। একে বলা যায় ঘুরতে ঘুরতে পাশেরদিকে হাটা। সপ্তম নকশায় চার রকমের প্রতিসাম্যতা রয়েছে(স্থানান্তর, উলম্ব ও অনুভূমিক রেখায় প্রতিফলন এবং ঘূর্ণন)এটার মোটিফে চার রকম প্রতিসাম্য রূপান্তর প্রয়োগ করায়ায় এবং একে বলা যায় ঘুরতে ঘুরতে লাফানো। একটা নির্দিষ্ট রূপান্তর পর্যায়ক্রমে হয়ে থাকে যার কারণে নকশা গুলো পর্যায়ক্রমিক নকশা। ফ্রেজপ্যাটার্ন সমূহ শুধু একটা রেখা বরাবর পুনরাবৃত্তি হয়ে থাকে তাই এগুলোকে বলা যায় একমাত্রিক নকশা কিন্তু দেয়ালের অথবা মেঝের কারুকার্যে যে নকশা সমূহ দেখা যায় সেগুলি দুই মাত্রিক ভাবে বিস্তৃত থাকে অর্থাৎ একটা মোটিফ দ্বিমাত্রিক তলে প্রতিসাম্য রূপান্তরের মাধ্যমে পুনরাবৃত্তি করে থাকে দ্বিমাত্রিক পর্যায়ক্রমিক নকশা রয়েছে ১৭ রকমের। এই দ্বিমাত্রিক নকশা সমূহে স্থানান্তর প্রতিসাম্যতা, ঘূর্ণন প্রতিসামতা (১৮০ ডিগ্রীতে, ১২০ ডিগ্রীতে, ৯০ডিগ্রীতে, এবং ৬০ডিগ্রীতে),গ্লাইডরিফ্লেকশন, উলম্ব ও অনুভূমিক রেখায় প্রতিফলন প্রতিসাম্যতা দেখাযায় এটা গাণিতিক ভাবে প্রমাণিত যে কোন পর্যায়ক্রমিক নকশা শুধু ১৮০ডিগ্রীতে, ১২০ডিগ্রীতে, ৯০ডিগ্রীতে, এবং ৬০ ডিগ্রীতে ঘূর্ণন রূপান্তরের মাধ্যমেই সম্ভব এদের বলা হয় ২ফোল্ড, ৩ফোল্ড, ৪ফোল্ড এবং ৬ফোল্ড ঘূর্ণন অক্ষ প্রতিসাম্য(n ফোল্ড=৩৬০/n)। ঘূর্ণন প্রতিসাম্যতা মানে যে পরিমাণ ঘুরালে কোন আকারকে একই রকম দেখায়। ১ফোল্ড প্রতিসাম্যতা আসলে কোন প্রতিসাম্যতা নয় কারণ একটা আকার যত অপ্রতিসমই হোক না কেন তা ৩৬০ ডিগ্রীতে ঘুরালে একইরকম দেখাবে। পর্যায়ক্রমিক নকশার বৈশিষ্ট্য হচ্ছে এরা একটা একক কোষ বা ইউনিট সেল পুনরাবৃত্তির মাধ্যমে গঠিত হয়ে থাকে ১৭ রকমের নকশায় মাত্র পাঁচ রকমের ইউনিট সেল দেখাযায়।কোন নকশায় মোটিফ গুলো সরিয়ে নিলে শুধু ইউনিট সেলের যে জাল পাওয়া যাবে তাকে বলে ল্যাটিস । ইউনিট সেলের শীর্ষবিন্দু(vertex) সমূহের বিন্যাসটা হচ্ছে ল্যাটিস আর শীর্ষবিন্দুগুলো হল ল্যাটিস বিন্দু। সতের রকমের নকশা পাঁচ রকম ল্যাটিস গঠন বিশিষ্ট হয়ে থাকে কোন নকশায় ৯০ ডিগ্রী ঘূর্ণন প্রতিসাম্যতা থাকলে তার ল্যাটিস অবশ্যই বর্গাকার হবে আবার যদি ৬০ ডিগ্রী ও ১৮০ডিগ্রী প্রতিসাম্যতা থাকে তাহলে ষড়ভুজাকার এবং উলম্ব রেখা প্রতিফলন প্রতিসম বিশিষ্ট নকশা সাধারণত আয়তাকার ল্যাটিস গঠন বিশিষ্ট হয়ে থাকে। নীচের চিত্রে সতের দ্বিমাত্রিক নকশা এবং তাদের একককোষ ও প্রতিসাম্যতা দেখানো হলো।


উপরে বর্ণিত ধারনা সমূহ যেমন মোটিফ,ইউনিট সেলের পুনরাবৃত্তি এবং সমান দূরত্বে সুষমভাবে বিন্যস্ত বিন্দু বা ল্যাটিস তিনমাত্রার ক্ষেত্রেও প্রযোজ্য । কিন্তু তিনমাত্রায় আরও বাড়তি কিছু প্রতিসাম্য রূপান্তর পাওয়া যায় যেমন স্ক্রু ঘূর্ণন অর্থাৎ একটা অক্ষের চারপাশে প্যাঁচানো নকশা আর ইনভার্সন এবং গ্লাইড প্ল্যান। এটা খুবই স্পষ্ট যে তিনমাত্রায় পরিস্থিতি আরও বেশী জটিল হবে এবং নকশার সংখ্যাও হবে দুইমত্রার চেয়ে অনেক বেশী। বিভিন্ন প্রতিসম রূপান্তর এবং এদের সমাবেশ থেকে মোট ২৩০ রকমের ত্রিমাত্রিক পর্যায়ক্রমিক নকশা তৈরি হয় আর মোট ল্যাটিসের সংখ্যা হচ্ছে চৌদ্দটি।দুইশতত্রিশ রকমের ত্রিমাত্রিক নকশায় মাত্র ১৪ রকমের ল্যাটিস গঠন পাওয়া যায়।এই ল্যাটিস সমূহকে বলা হয় ব্রাভেইস ল্যাটিস।ত্রিমাত্রিক ল্যাটিসের ধারনা প্রথম প্রদান করেন ফ্রাঙ্কেইনহাইম নামে এক ব্যাক্তি তার প্রস্তাবিত ল্যাটিসের সংখ্যা ছিল পনেরটা কিন্তু দুর্ভাগ্যবশত দুইটি ল্যাটিস একরকম ছিল। পরবর্তীতে ব্রাভেইস ব্যাপারটা ধরতে পারেন যে ল্যাটিস আসলে চৌদ্দটি তাই এই ল্যাটিসগুলোকে এখন ব্রাভেইস ল্যাটিস বলা হয়। ব্রাভেইস ল্যাটিস দুই প্রকার প্রিমিটিভ এবং সেন্টারেড।  একমাত্রিকে ৭ দুইমাত্রায় ১৭ এবং তিনমাত্রায় ২৩০টি প্রতিসাম্য দল থাকলে প্রশ্ন উঠতে পারে যে চতুর্মাত্রায় প্রতিসাম্য দল কয়টি?।আরও সাধারণ ভাবে বলা যায় যে n(n=১,২,৩…… n)মাত্রায় কি সবসময়ই এরকম সসীম সংখ্যক প্রতিসম রূপান্তর পাওয়া যাবে। ১৯১০ সালে এই প্রশ্নের ইতিবাচক উত্তর পাওয়াযায়। ১৯৭০ সালে এটাও প্রমাণিত হয় যে চতুর্মাত্রায় প্রতিসম রূপান্তর ৪৭৮৩টি। চতুর্মাত্রায় ব্রাভেইস ল্যাটিস ৬৪টি।প্রাকৃতিক ভাবে প্রাপ্ত ত্রিমাত্রিক নকশার ভালো উদাহরণ হচ্ছে ভূত্বক থেকে প্রাপ্ত নির্দিষ্ট পারমাণবিক সজ্জা বিশিষ্ট উপাদান বা মিনারেল। মিনারেলের বৈশিষ্ট্য হচ্ছে এদের পারমাণবিক গঠন নির্দিষ্ট সজ্জা বিশিষ্ট হয়ে থাকে। এই উপাদান গুলো কেলাস গঠনসমৃদ্ধ । কেলাস গঠিত হয়ে থাকে কোন মোটিফ এর ত্রিমাত্রিক পর্যায়ক্রমিক পুনরাবৃত্তির মাধ্যমে। কোয়ার্টজ হচ্ছে এ ধরনের মিনারেল যার কেলাস গঠন রয়েছে। কোয়ার্টজের মোটিফ গঠিত হয় তিনটি সিলিকন পরমাণুর সমন্বয়ে। তিনটি সিলিকন পরমাণু দ্বারা গঠিত চতুস্থলকিয় মোটিফ পুনরাবৃত্তির মাধ্যমে কেলাস তৈরি হয়ে থাকে। কোয়ার্টজের ইউনিটসেল রম্বোহেড্রাল।
একমাত্রিকে ৭ দুইমাত্রায় ১৭ এবং তিনমাত্রায় ২৩০টি প্রতিসাম্য দল থাকলে প্রশ্ন উঠতে পারে যে চতুর্মাত্রায় প্রতিসাম্য দল কয়টি?।আরও সাধারণ ভাবে বলা যায় যে n(n=১,২,৩…… n)মাত্রায় কি সবসময়ই এরকম সসীম সংখ্যক প্রতিসম রূপান্তর পাওয়া যাবে। ১৯১০ সালে এই প্রশ্নের ইতিবাচক উত্তর পাওয়াযায়। ১৯৭০ সালে এটাও প্রমাণিত হয় যে চতুর্মাত্রায় প্রতিসম রূপান্তর ৪৭৮৩টি। চতুর্মাত্রায় ব্রাভেইস ল্যাটিস ৬৪টি।প্রাকৃতিক ভাবে প্রাপ্ত ত্রিমাত্রিক নকশার ভালো উদাহরণ হচ্ছে ভূত্বক থেকে প্রাপ্ত নির্দিষ্ট পারমাণবিক সজ্জা বিশিষ্ট উপাদান বা মিনারেল। মিনারেলের বৈশিষ্ট্য হচ্ছে এদের পারমাণবিক গঠন নির্দিষ্ট সজ্জা বিশিষ্ট হয়ে থাকে। এই উপাদান গুলো কেলাস গঠনসমৃদ্ধ । কেলাস গঠিত হয়ে থাকে কোন মোটিফ এর ত্রিমাত্রিক পর্যায়ক্রমিক পুনরাবৃত্তির মাধ্যমে। কোয়ার্টজ হচ্ছে এ ধরনের মিনারেল যার কেলাস গঠন রয়েছে। কোয়ার্টজের মোটিফ গঠিত হয় তিনটি সিলিকন পরমাণুর সমন্বয়ে। তিনটি সিলিকন পরমাণু দ্বারা গঠিত চতুস্থলকিয় মোটিফ পুনরাবৃত্তির মাধ্যমে কেলাস তৈরি হয়ে থাকে। কোয়ার্টজের ইউনিটসেল রম্বোহেড্রাল।
ক্রিস্টালোগ্রাফিঃ বিজ্ঞানের যে শাখায় কেলাসের গঠন বৈশিষ্ট্য ইত্যাদি নিয়ে আলোচনা করা হয় তাকে বলে ক্রিস্টালোগ্রাফি(Crystallography)। ক্রিস্টালোগ্রাফির জন্ম হয় এক্সরে আবিষ্কারের পর। ১৯১৩ সালের দিকে জার্মান পদার্থবিজ্ঞানী ম্যাক্স ভন লাউ এক্সরে রশ্মি কে কেলাসের মধ্যে দিয়ে চালিত করে অপবর্তন ঝালর দেখতে পান এরপর হেনরি ব্র্যাগ এবং তার পুত্র লরেন্স ব্র্যাগ কেলাসের এক্সরে অপবর্তন ঝালরের সাথে পারমাণবিক গঠনপ্রকৃতির সম্পর্ককে সূত্রবদ্ধ করেন যা এক্সরে অপবর্তনকে পদার্থের গঠন বুঝবার একটা শক্তিশালী হাতিয়ারে পরিণত করে। ১৯১৫ সালে পিতা ও পুত্রকে একসাথে পদার্থবিজ্ঞানে নোবেল পুরষ্কার দেওয়া হয়। একটা জলাশয়ের কথা ভাবতে পারি যার মধ্যে কিছু গাছ রয়েছে এখন বাতাসে যদি এই জলাশয়ের উপরিতলে সমান্তরাল ঢেউ সৃষ্টি করে তাহলে ঢেউগুলো যখন গাছের গোড়ায় আঘাত করবে তখন প্রত্যেকটা গাছকে কেন্দ্র করে বৃত্তাকার তরঙ্গ মুখ সৃষ্ট হবে ধীরে ধীরে এই বৃত্তাকার তরঙ্গ মুখ সমূহ প্রসারিত হয়ে একটা আরেকটার সাথে ব্যতিচার ঘটাবে।কেলাসের ক্ষেত্রেও অনুরূপ ব্যাপার ঘটে থাকে। যখন এক্সরে তরঙ্গ কেলাসের ভেতর পাঠানো হয় তখন প্রত্যেকটা পরমাণু গোলাকার তরঙ্গ মুখ তৈরি করে যারা একে অন্যের সাথে ব্যতিচার ঘটায় ব্যতিচারিত তরঙ্গ মুখের চিত্র একটা ফটোগ্রাফিক প্লেটে ধারণ করা হয় যা থেকে কেলাসের অভ্যন্তরীণ গঠন জানা যায়। এই অপবর্তন ঝালরের জ্যামিতিক রূপ নির্ধারিত হয় পরমাণুগুলো কিভাবে বিন্যাস্ত তা দ্বারা অর্থাৎ যে নকশায় সজ্জিত তার ল্যাটিস গঠন দ্বারা। এক্সরে অপবর্তন আবিষ্কারের আগে কেলাস সম্পর্কে জানা যেত শুধু বাইরের জ্যামিতিক আকার থেকে।এক্সরে ছারাও ইলেকট্রন এবং নিউট্রন রশ্মি অপবর্তন ব্যাবহার করা হয়ে থাকে। ক্রিস্টালোগ্রাফির অধ্যয়নের মূল ভিত্তি হিসেবে রয়েছে প্যাটার্ন থিওরি।বিজ্ঞানের বিভিন্ন শাখায় ক্রিস্টালোগ্রাফির গুরুত্বপূর্ণ প্রয়োগ রয়েছে পদার্থবিদ্যা,রসায়ন,আণবিক জীববিজ্ঞান,মিনারলজি এবং কঠিন অবস্থার পদার্থবিজ্ঞান বা সলিড স্টেট ফিজিক্সের মূল ভিত্তি হিসেবে রয়েছে ক্রিস্টালোগ্রাফি। ২০১৩ সালে ক্রিস্টালোগ্রাফির একশত বৎসর উদযাপন করা হয় ২০১২ সালের জুলাইয়ে জাতিসংঘ ২০১৪ সালকে আন্তর্জাতিক ক্রিস্টালোগ্রাফিক বছর হিসেবে ঘোষণা করে। ১৯৮৪ সালের আগে পর্যন্ত মনেকরা হতো কেলাসীয় গঠন সবসময়ই পর্যায়ক্রমিক হবে অর্থাৎ পরমাণুর একটা নির্দিষ্ট সজ্জা ত্রিমাত্রিক পুনরাবৃত্তির মাধ্যমে কেলাস গঠন করে। ১৯৮৪ সালে ইসরাইলী বিজ্ঞানী ড্যান শেচতম্যান অ্যালুমিনিয়াম-ম্যাঙ্গানিজ সঙ্করের অপবর্তন ঝালর বিশ্লেষণ করে দেখতে পান যে এর অভ্যন্তরীণ গঠনে ৩৬ডিগ্রী ঘূর্ণন প্রতিসাম্যতা রয়েছে যার মানে ১০ফোল্ড ঘূর্ণন প্রতিসাম্যতা। একটি নির্দিষ্ট ইউনিটসেল পুনরাবৃত্তির মাধ্যমে গঠিত কেলাসে শুধু ২,৩,৪,৬ ফোল্ড ঘূর্ণন প্রতিসাম্যতা সম্ভব ৫,১০ফোল্ড সম্ভব নয় আবার যেহেতু অপবর্তন ঝালরে ১০ফোল্ড প্রতিসাম্যতা দেখাচ্ছে তারমানে এর গঠন একেবারে অপ্রতিসম বিশৃঙ্খলও নয় তাহলে পরমাণু গুলো আসলে কিভাবে সজ্জিত?। অ্যালুমিনিয়াম-ম্যাঙ্গানিজ সঙ্কর যার নামকরণ করা হয় শেচতম্যানাইট আসলে কোয়াসিপেরিয়ডিক বা অর্ধ-পর্যায়ক্রমিক গঠন বিশিষ্ট যাদের বলা হয় কোয়াসিক্রিস্টাল বা কোয়াসিকেলাস এদের ল্যাটিস গঠন হচ্ছে কোয়াসিল্যাটিস। শেচতম্যানের আবিষ্কার দুই বছর পর্যন্ত অপ্রকাশিত রইলো তার নিজের সতর্কতার এবং পত্রিকা সম্পাদকদের সন্দেহের কারণে। ২০১১ সালে শেচতম্যানকে কোয়াসিকেলাস আবিষ্কারের জন্য রসায়নে নোবেল পুরস্কার দেয়া হয়।
এক্সরে অপবর্তন আবিষ্কারের আগে কেলাস সম্পর্কে জানা যেত শুধু বাইরের জ্যামিতিক আকার থেকে।এক্সরে ছারাও ইলেকট্রন এবং নিউট্রন রশ্মি অপবর্তন ব্যাবহার করা হয়ে থাকে। ক্রিস্টালোগ্রাফির অধ্যয়নের মূল ভিত্তি হিসেবে রয়েছে প্যাটার্ন থিওরি।বিজ্ঞানের বিভিন্ন শাখায় ক্রিস্টালোগ্রাফির গুরুত্বপূর্ণ প্রয়োগ রয়েছে পদার্থবিদ্যা,রসায়ন,আণবিক জীববিজ্ঞান,মিনারলজি এবং কঠিন অবস্থার পদার্থবিজ্ঞান বা সলিড স্টেট ফিজিক্সের মূল ভিত্তি হিসেবে রয়েছে ক্রিস্টালোগ্রাফি। ২০১৩ সালে ক্রিস্টালোগ্রাফির একশত বৎসর উদযাপন করা হয় ২০১২ সালের জুলাইয়ে জাতিসংঘ ২০১৪ সালকে আন্তর্জাতিক ক্রিস্টালোগ্রাফিক বছর হিসেবে ঘোষণা করে। ১৯৮৪ সালের আগে পর্যন্ত মনেকরা হতো কেলাসীয় গঠন সবসময়ই পর্যায়ক্রমিক হবে অর্থাৎ পরমাণুর একটা নির্দিষ্ট সজ্জা ত্রিমাত্রিক পুনরাবৃত্তির মাধ্যমে কেলাস গঠন করে। ১৯৮৪ সালে ইসরাইলী বিজ্ঞানী ড্যান শেচতম্যান অ্যালুমিনিয়াম-ম্যাঙ্গানিজ সঙ্করের অপবর্তন ঝালর বিশ্লেষণ করে দেখতে পান যে এর অভ্যন্তরীণ গঠনে ৩৬ডিগ্রী ঘূর্ণন প্রতিসাম্যতা রয়েছে যার মানে ১০ফোল্ড ঘূর্ণন প্রতিসাম্যতা। একটি নির্দিষ্ট ইউনিটসেল পুনরাবৃত্তির মাধ্যমে গঠিত কেলাসে শুধু ২,৩,৪,৬ ফোল্ড ঘূর্ণন প্রতিসাম্যতা সম্ভব ৫,১০ফোল্ড সম্ভব নয় আবার যেহেতু অপবর্তন ঝালরে ১০ফোল্ড প্রতিসাম্যতা দেখাচ্ছে তারমানে এর গঠন একেবারে অপ্রতিসম বিশৃঙ্খলও নয় তাহলে পরমাণু গুলো আসলে কিভাবে সজ্জিত?। অ্যালুমিনিয়াম-ম্যাঙ্গানিজ সঙ্কর যার নামকরণ করা হয় শেচতম্যানাইট আসলে কোয়াসিপেরিয়ডিক বা অর্ধ-পর্যায়ক্রমিক গঠন বিশিষ্ট যাদের বলা হয় কোয়াসিক্রিস্টাল বা কোয়াসিকেলাস এদের ল্যাটিস গঠন হচ্ছে কোয়াসিল্যাটিস। শেচতম্যানের আবিষ্কার দুই বছর পর্যন্ত অপ্রকাশিত রইলো তার নিজের সতর্কতার এবং পত্রিকা সম্পাদকদের সন্দেহের কারণে। ২০১১ সালে শেচতম্যানকে কোয়াসিকেলাস আবিষ্কারের জন্য রসায়নে নোবেল পুরস্কার দেয়া হয়।


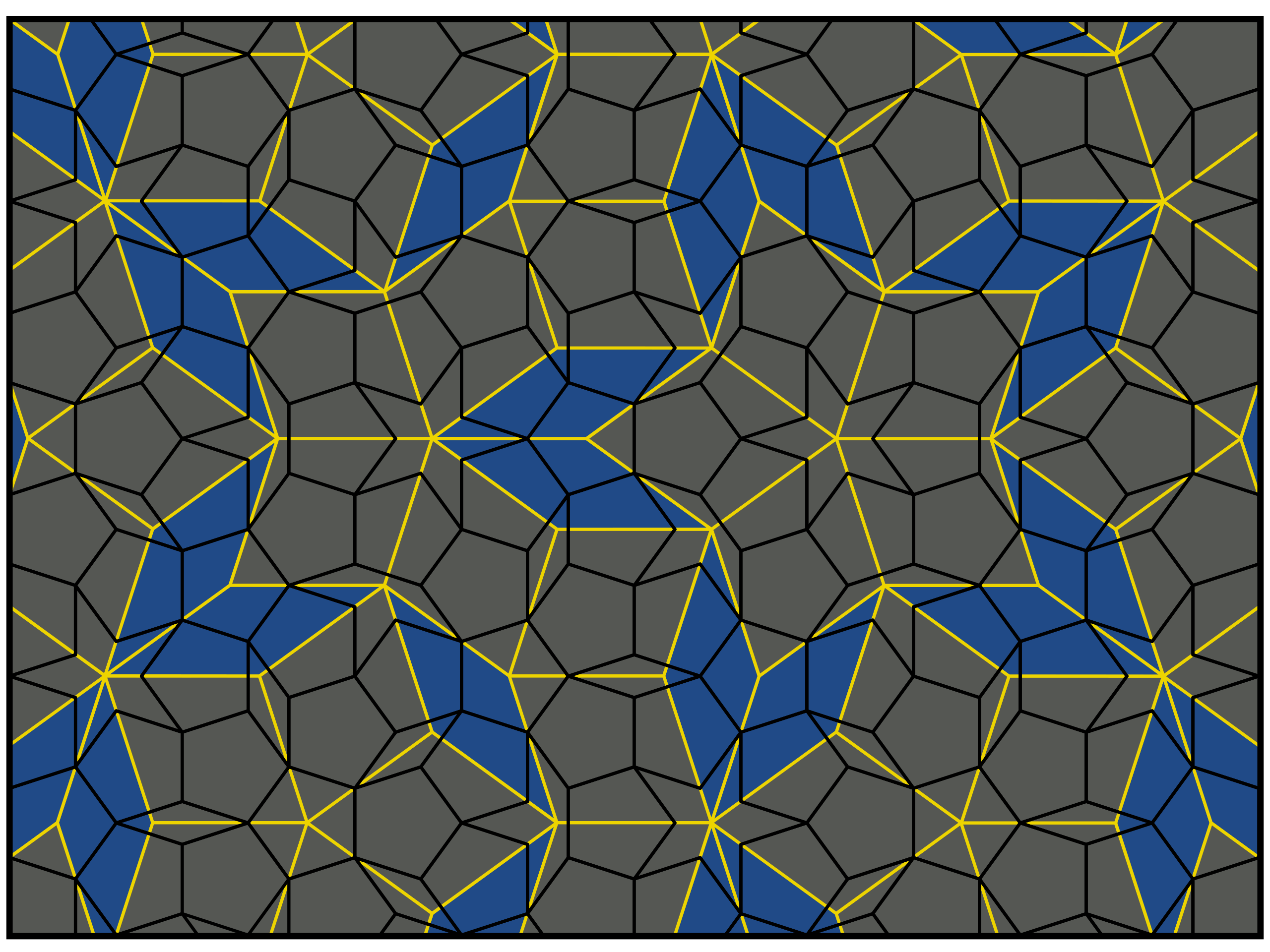
টাইলিং এবং কোয়াসিকেলাসঃ কোয়াসিকেলাস আবিষ্কারের অনেক আগে থেকেই টাইলিং থিওরিতে অর্ধ-পর্যায়ক্রমিক গঠন পাওয়া গিয়েছিল।টাইলিং একটা প্রাচীন বিষয় শিল্প এবং স্থাপত্যে এর ব্যাপক ব্যাবহার দেখা যায় বিশেষ করে প্রাচীন ইসলামিক স্থাপত্যে। কোন স্থানকে কিভাবে নির্দিষ্ট কিছু আকার দিয়ে ঢেকে ফেলা যায় সেটাই এর আলোচ্য বিষয় বিনোদনমূলক গনিতে(Recreational mathematics)একটি উল্লেখযোগ্য বিষয় টাইলিং। নির্দিষ্ট আকারের কিছু টালির সেটের প্রতিলিপি দ্বারা কোন স্থানকে ঢেকেফেলা গেলে ঐ সেটকে বলে প্রটোসেট এবং উপাদান গুলো হল প্রোটোটাইল যেমন একইরকম বর্গক্ষেত্র দ্বারা টাইলিং করা মেঝেতে প্রোটোটাইল সংখ্যা একটি একই রকম দেখতে বর্গাকার টালি দ্বারা মেঝেকে টাইলিং করা হয়েছে অর্থাৎ সব টালি একটি বর্গাকার প্রটোটাইলের প্রতিলিপি।আবার দাবা বোর্ডে দুই রং এর বর্গ, বর্গাকার হলেও তারা রঙে ভিন্ন এই ভিন্নতা বিবেচনা করলে বলা যায় প্রটোটাইল সংখ্যা দুই। একটা টাইলিং এ সসীম সংখ্যক প্রোটোটাইলের প্রতিলিপি দ্বারা অসীম বিস্তৃত স্থান টাইলিং করা যায় তবে সাধারণ কোন এলগরিদম নেই যার মাধ্যমে জানা সম্ভব কোন আকার দ্বারা টাইলিং হবে কি হবে না । কোন টাইলিংকে পর্যায়ক্রমিক বলা হয় যদি এমন একটি আকার পাওয়া যায় যেটা বার বার পুনরাবৃত্তি হয়েছে অর্থাৎ সব যায়গাতেই ঐ আকার পাওয়া যাবে একই আকার স্থানান্তর এর মাধ্যমে এ ধরনের টাইলিং তৈরি করা যায় তাই পর্যায়ক্রমিক টাইলিংএ স্থানান্তর প্রতিসাম্যতা থাকে। উদাহরণ সরূপ নীচের চিত্রে বিখ্যাত ডাচ চিত্রশিল্পী এম সি এচার এর (যিনি তার অংকনে বিভিন্ন টাইলিং থেকে ছবি তৈরি করতেন) চিত্রকর্ম দেখা যাচ্ছে যেখানে পর্যায়ক্রমিক টাইলিং এর প্রটোটাইল দুটি সাদা এবং কালো পাখি । এখানে সাদা এবং কালো পাখির মিলিত একটি আকার যা বার বার পুনরাবৃত্তি হয়েছে কোন টাইলিংএ এই ধরনের কোন আকার যদি না থাকে তাহলে তা অপর্যায়ক্রমিক। কোয়াসিকেলাসের জ্যামিতিক গঠন অপর্যায়ক্রমিক টাইলিং এর মতো হয়ে থাকে কোয়াসিকেলাসের গাণিতিক মডেলে দ্বিমাত্রিক পেনরোজ টাইলিং এর ত্রিমাত্রিক সংস্করণ ব্যাবহার করা হয়। অপর্যায়ক্রমিক টাইলিং এর একটি সেট প্রথম আবিষ্কৃত হয় ১৯৬৬ সালে যেটার প্রটোটাইল সংখ্যা ছিল ২০২৪৬টি পরবর্তীতে উদ্ভাবক প্রটোটাইল সংখ্যা ১০৪টিতে কমিয়ে আনেন।পরে আরেকজন গবেষক ৪০টি প্রটোটাইল দিয়ে একটি অপর্যায়ক্রমিক টাইলিং আবিষ্কার করেন ১৯৭১ সালে রবীনসন নামে আরেকজন একটি অপর্যায়ক্রমিক টাইলিং উদ্ভাবন করেন যার প্রটোটাইল ৬টি ১৯৭৪ সালে গাণিতিক পদার্থবিদ রজার পেনরোজ একটি অপর্যায়ক্রমিক টাইলিং উদ্ভাবন করেন যার প্রটোটাইল মাত্র দুইটি যা পরবর্তীতে পেনরোজ টাইলিং নামে পরিচিতি লাভ করে । দুই ধরনের প্রটোসেট দ্বারা পেনরোজ টাইলিং তৈরি করা যায় একটা ধরন হচ্ছে “কাইট”এবং“ডার্ট” নামক দুটি প্রটোটাইল এই দুই প্রটোটাইল ম্যাচিংরুল অনুসারে সজ্জিত করে পেনরোজের অপর্যায়ক্রমিক টাইলিং পাওয়া যায়।টাইলিং এর সময় প্রটোটাইল কিভাবে বসাতে হবে তা ম্যাচিংরুল থেকে পাওয়া যায়।নিচের চিত্রে কাইট এবং ডার্ট এবং এদের কোনায় সাদা এবং কালো বিন্দু ম্যাচিংনিয়ম অনুসারে কালো বিন্দু সবসময় সাদা বিন্দুতে মিলত হবে।দ্বিতীয় ধরনের প্রোটোসেটে রয়েছে মোটা এবং পাতলা রম্বস নির্দিষ্ট ম্যাচিং রুল যা রম্বসের বাহুতে তীর চিহ্ন দিয়ে বুঝানো হয়েছে। কাইট ও ডার্ট এবং মোটা ও পাতলা রম্বস জ্যামিতিক ভাবে সম্পর্কিত যেমন একটি কাইট এবং ডার্ট জোরা দিয়ে একটা মোটা রম্বস তৈরিকরা যায় আবার একটা কাইট কে মাঝখান দিয়ে দ্বিখণ্ডিত করে যে ত্রিভুজ পাওয়া যায় তা জোড়া লাগিয়ে পাতলা রম্বস তৈরি করা যায় এরা আসলে একই টাইলিং এর দুটি ভিন্ন প্রোটোসেট। পেনরোজ টাইলিংএ একই আকার বার বার বিভিন্ন দূরত্বে (সবখানে নয়)পুনরাবৃত্ত হয় কারণ এটা আসলে অর্ধপর্যায়ক্রমিক বা কোয়াসি পেরিয়ডিক। এল্যান ম্যাকি নামে এক ক্রিস্টালোগ্রাফার দেখানযে আমারা যদি পেনরোজ টাইলিং এর প্রত্যেক টাইলের শীর্ষ বিন্দু তে আলোক বিক্ষেপণ স্থাপন করে অপবর্তন ঝালর নেই তাহলে ঐ অপবর্তন ঝালরে ১০ফোল্ড ঘূর্ণন প্রতিসাম্যতা থাকবে।গবেষণায় আরও দেখাযায় যে অপবর্তন ঝালরের এই ১০ফোল্ড ঘূর্ণন প্রতিসাম্যতা প্রত্যেক বিন্দুতে বিক্ষেপকের অবস্থানের সাথে আলাদা ভাবে সম্পর্কিত নয় বরং এদের সামগ্রিক অবস্থানের পরিসংখ্যানিক গুনাগুণের সাথে সম্পর্কিত।এই ব্যাপার থেকে একটা ধারনা পাওয়া যায় যে অর্ধপর্যায়ক্রমিকতার মধ্যে পর্যায়ক্রমিকতার মতো সুষম প্রতিসাম্যতা না থকলেও নতুন ধরনের প্রতিসাম্যতা থাকে যাকে বলা হয় পরিসংখ্যানিক প্রতিসাম্যতা(Statistical symmetry) যা অপবর্তন ঝালরে প্রকাশিত হয়।ত্রিমাত্রিক কোয়াসিকেলাস অপবর্তন ঝালরে যখন ১০ফোল্ড ঘূর্ণন প্রতিসাম্যতা পাওয়া যায় যার অর্থ এর অভ্যন্তরে দ্বিমাত্রিক পেনরোজ টাইলিংএর মতো পরিসংখ্যানিক প্ররতিসাম্যতা রয়েছে। শেচতম্যান যখন অ্যালুমিনিয়াম ম্যাঙ্গানিজ খাদের অপবর্তনে ১০ফোল্ড প্রতিসাম্যতা দেখে ধাঁধায় পরেছিলেন তখন আরও দুজন বিজ্ঞানী স্টাইনহারডট এবং লেভীন একধরনের ত্রিমাত্রিক জ্যামিতিক আকারের অপবর্তন ঝালরে একই ১০ফোল্ড প্রতিসাম্যতা পেয়েছিলেন তাদের জ্যামিতিক গঠনটা ছিল ত্রিমাত্রিক স্থানে দুই রকমের রম্বহ্যড্রা দিয়ে তৈরি এক ধরনের ত্রিমাত্রিক টাইলিং যা পেনরোজের মোটা ও পাতলা রম্বসের ত্রিমাত্রিক রূপ। কোয়াসি কেলাসের জ্যামিতিক গঠনের সাথে ত্রিমাত্রিক পেনরোজ টাইলিং এর সাদৃশ্য পাওয়া যায়।
এল্যান ম্যাকি নামে এক ক্রিস্টালোগ্রাফার দেখানযে আমারা যদি পেনরোজ টাইলিং এর প্রত্যেক টাইলের শীর্ষ বিন্দু তে আলোক বিক্ষেপণ স্থাপন করে অপবর্তন ঝালর নেই তাহলে ঐ অপবর্তন ঝালরে ১০ফোল্ড ঘূর্ণন প্রতিসাম্যতা থাকবে।গবেষণায় আরও দেখাযায় যে অপবর্তন ঝালরের এই ১০ফোল্ড ঘূর্ণন প্রতিসাম্যতা প্রত্যেক বিন্দুতে বিক্ষেপকের অবস্থানের সাথে আলাদা ভাবে সম্পর্কিত নয় বরং এদের সামগ্রিক অবস্থানের পরিসংখ্যানিক গুনাগুণের সাথে সম্পর্কিত।এই ব্যাপার থেকে একটা ধারনা পাওয়া যায় যে অর্ধপর্যায়ক্রমিকতার মধ্যে পর্যায়ক্রমিকতার মতো সুষম প্রতিসাম্যতা না থকলেও নতুন ধরনের প্রতিসাম্যতা থাকে যাকে বলা হয় পরিসংখ্যানিক প্রতিসাম্যতা(Statistical symmetry) যা অপবর্তন ঝালরে প্রকাশিত হয়।ত্রিমাত্রিক কোয়াসিকেলাস অপবর্তন ঝালরে যখন ১০ফোল্ড ঘূর্ণন প্রতিসাম্যতা পাওয়া যায় যার অর্থ এর অভ্যন্তরে দ্বিমাত্রিক পেনরোজ টাইলিংএর মতো পরিসংখ্যানিক প্ররতিসাম্যতা রয়েছে। শেচতম্যান যখন অ্যালুমিনিয়াম ম্যাঙ্গানিজ খাদের অপবর্তনে ১০ফোল্ড প্রতিসাম্যতা দেখে ধাঁধায় পরেছিলেন তখন আরও দুজন বিজ্ঞানী স্টাইনহারডট এবং লেভীন একধরনের ত্রিমাত্রিক জ্যামিতিক আকারের অপবর্তন ঝালরে একই ১০ফোল্ড প্রতিসাম্যতা পেয়েছিলেন তাদের জ্যামিতিক গঠনটা ছিল ত্রিমাত্রিক স্থানে দুই রকমের রম্বহ্যড্রা দিয়ে তৈরি এক ধরনের ত্রিমাত্রিক টাইলিং যা পেনরোজের মোটা ও পাতলা রম্বসের ত্রিমাত্রিক রূপ। কোয়াসি কেলাসের জ্যামিতিক গঠনের সাথে ত্রিমাত্রিক পেনরোজ টাইলিং এর সাদৃশ্য পাওয়া যায়।
গাণিতিকভাবে দেখা যায় কোয়াসিকেলাসের অর্ধপর্যায়ক্রমিক গঠন অতিমাত্রিক পর্যায়ক্রমিক গঠনের ত্রিমাত্রিক অভিক্ষেপ বা ছায়া।নিন্ম মাত্রার অর্ধপর্যায়ক্রমিক গঠন উচ্চমাত্রার পর্যায়ক্রমিক গঠনের অভিক্ষেপ হিসেবে বর্ণনা করা যায়। দ্বি এবং ত্রি মাত্রার পর্যায়ক্রমিক গঠনে ১০ফোল্ড প্রতিসাম্যতা অসম্ভব হলেও ছয় মাত্রায় সম্ভব।দুই মাত্রার পেনরোজ টাইলিং আসলে পাঁচ মাত্রার হাইপার কিউব গঠনের দ্বিমাত্রিক স্লাইস।এই দৃষ্টিভঙ্গি অনুযায়ী বলা যায় কোয়াসিপেরিয়ডিক কেলাস আসলে পেরিয়ডিক কিন্তু আমাদের ত্রিমাত্রিক জগতে তা অর্ধপর্যায়ক্রমিক মনেহয় অর্থাৎ কেলাস আর কোয়াসিকেলাসে পার্থক্য হল একটা ত্রিমাত্রিক পর্যায়ক্রমিক আর আরেকটা আতিমাত্রিক পর্যায়ক্রমে গঠিত।
তথ্যসূত্র:
- The Basics of Crystallography
By Christopher Hammond - QUASICRYSTALS AND GEOMETRY
By Marjorie Senechal - Symmetry through the Eyes of a Chemist
By Magdolna Hargittai and Istv´an Hargittai - Introduction to mineral sciences
By Andrew putnis - The mathematical century
By Piergiorgio Odifreddi - https://www.uwgb.edu/dutchs/symmetry/2dspcgrp.htm
- http://www.metafysica.nl/groups/index_a2a.html
- http://www.quartzpage.de/
- https://www.wikipedia.org/







Leave a Reply to আরাফাত রহমানCancel reply