
১৯ শতকের প্রথমদিকেও গণিতবিদদের মহলে শূন্যের শূন্যতম ঘাত বা সূচক $(0^0)$ এর ব্যাখ্যা একটি বিতর্কের বিষয় ছিল। সেসময়কার অধিকাংশ গণিতবিদেরা মেনে নিয়েছিলেন $0^0=1$। কিন্তু সমস্যা বেধেছিল, ১৮২১ সালে গণিতবিদ Cauchy $0^0$ কে $\frac{0}{0}$ এর মত অনির্ণেয় আকারগুলোর সাথে একই তালিকাভুক্ত করলেন। আবার ১৮৩০ এর দশকে গণিতবিদ Libri $0^0=1$ এর পক্ষে তার যুক্তি প্রকাশ করেছিলেন। সেটাও ছিল সংশয়পূর্ণ, কিন্তু আরেক গণিতবিদ Möbius তাঁকে সমর্থন দিয়েছিলেন এবং ভুলভাবে দাবি করেছিলেন যে, $\displaystyle\lim_{t \to 0^{+}} f(t) = \displaystyle\lim_{t \to 0^{+}} g(t) = 0$ হলেই $\displaystyle\lim_{t \to 0^{+}} {f(t)}^{g(t)} = 1$ হয়। একজন ব্যাখাকারী (যিনি শুধুমাত্র ‘S’ দিয়ে নাম স্বাক্ষর দিয়েছিলেন) এর প্রতিউত্তরে ${(e^{-1/t})}^t$ এর উদাহরণ দিয়েছিলেন এবং ফলস্বরূপ এই বাক-বিতণ্ডা কিছু সময়ের জন্য হলেও একটু শীথিল হয়েছিল। যা হোক, অনেক তর্ক-বিতর্ক, দ্বিধা-দ্বন্দ শেষে ১৯৯২ সালে গণিতবিদ Donald Knuth এ ব্যাপারটি শক্তপোক্ত গাণিতিক যুক্তি দিয়ে সুস্পষ্ট করলেন যে, $0^0$ কে $1$ হতেই হবে। সেই সাথে তিনি $0^0$ এর মান (value) এবং সীমাস্থ আকারের (liming form) মধ্যে পার্থক্য করেদিলেন। নির্ধারণ করে দিলেন, $0^0$ এর মান (the value $0^0$) হবে $1$ যেমনটা বলেছিলেন Libri এবং $0^0$ এর সীমাস্থ আকারকে (the limiting form $0^0$) অগত্যাই বলতে হবে অনির্ণেয় যেমনটা করেছিলেন Cauchy।
বোধ হয় ইতিহাস একটু বেশি হয়ে গেল যদিও গণিতবিদ Knuth এর গবেষণাপত্র আজকের এ লেখার বিষয়বস্তু নয়। এ লেখায় আমরা দেখব শিক্ষিত মহলের বিভিন্ন শ্রেণির পণ্ডিতেরা নিজেদের জ্ঞান ব্যবহার করে $0^0$ কে কিভাবে ব্যাখ্যা করেন। তাহলে চলুন দেরি না করে একে একে নিম্ন পর্যায় থেকে উচ্চ পর্যায়ের পণ্ডিতদের বক্তব্য শোনা (পড়া) যাক।

চালাক ছাত্রের বক্তব্য:
এটা তো খুব সহজ। আমি এটা জানি !
এই যে দেখুন $x^{0} = x^{1-1} = x^{1} x^{-1} = \frac{x}{x} = 1$
এখন আমরা এখানে $x=0$ বসালে পেয়ে যাব, $0^0$ এর মান হচ্ছে $1$ !
অতি চালাক ছাত্রের বক্তব্য:
না, তুমি ভুল করেছ! গণিতে শূন্য দিয়ে ভাগ করার কোন অনুমতি নেই, আর তুমি সেই অমান্য কাজটাই করে ফেলেছ। এজন্য এটাকে সমাধান করতে হবে এইভাবেঃ
$0^{x} = 0^{1+x-1} = 0^{1} \times 0^{x-1} = 0 \times 0^{x-1} = 0$
এটা সত্য, কারণ যেকোন কিছুকে শূন্য দিয়ে গুণ করলে গুণফল হয় শূন্য। এর অর্থ হল $0^{0} = 0$
অত্যাধিক চালাক ছাত্রের বক্তব্য:
ওটাতেও কাজ হবে না। কারণ যখন $x=0$ হয় তখন
$0^{x-1}$ অর্থাৎ $0^{-1} = \frac{1}{0}$
তাই তুমিও অজান্তেই তোমার তৃতীয় ধাপে শূন্য দিয়ে ভাগ করার সেই অমান্য কাজটা করে ফেলেছ! এর চেয়ে উত্তম উপায় হবে, আমরা $x^{x}$ ফাংশনটি নিয়ে চিন্তা করি এবং দেখি কী হয় যখন $x\,(x>0)$ ছোট হতে থাকে।
দেওয়া আছে, $$\begin{align*} \displaystyle\lim_{x \to 0^{+}} x^{x} &= \lim_{x \to 0^{+}} e^{(\ln{x^x})} \\&= \lim_{x \to 0^{+}} e^{(x\ln{x})} \\&=e^{\small{\left(\displaystyle \lim_{x \to 0^{+} } x\ln x \right)}} \\&= e^{\small{\left(\displaystyle\lim_{x \to 0^{+} } \frac{\ln x}{x^{-1}} \right)}} \\&= e^{\small{\left(\displaystyle\lim_{x \to 0^{+} } \frac{\frac{d}{dx}\ln x}{\frac{d}{dx}x^{-1}} \right)}} \\&= e^{\small{\left( \displaystyle\lim_{x \to 0^{+} } \frac{x^{-1}}{-x^{-2}} \right)}} \\&= e^{\small{\left( \displaystyle\lim_{x \to 0^{+}} -x \right)}} \\&= e^0 \\&= 1 \end{align*}$$
তাই যেহেতু $\displaystyle\lim_{x \to 0^{+}} x^{x} = 1$, সেহেতু আমি বলতে পারি, $0^{0} = 1$।
মাধ্যমিক বিদ্যালয়ের শিক্ষকের বক্তব্য:
হ্যাঁ, তুমি ঠিক বলেছ, $x$ এর ধনাত্বক মান যতই $0$ এর কাছাকাছি যেতে থাকে $x^x$ এর মান ততই $1$ এর কাছাকাছি আসতে থাকে। কিন্তু এটা ব্যবহার করে তুমি বলতে পারবে না যে $0^{0} = 1$ হয়। কারণ $x$ চলকের মান $0$ এর খুব কাছাকাছি হওয়া এবং পুরোপুরি $0$ হওয়া একই কথা নয়। এটা দেখা যাচ্ছে যে $0^0$ হচ্ছে অসংজ্ঞায়িত (undefined)। অর্থাৎ $0^0$ এর কোন মানই নেই।
ক্যালকুলাস শিক্ষকের বক্তব্য:
$x$ এর যেকোন ধনাত্বক মান $(x>0)$ নিয়ে আমরা লিখতে পারি, $0^{x} = 0$
অর্থাৎ $\displaystyle\lim_{x \to 0^{+}} 0^{x} = 0$
তাই, $x$ এর মান ধনাত্বক দিক থেকে যতই শূন্যের কাছে আনা হোক না কেন, $0^x$ এর মান শূন্যই হবে।
অপর দিকে, যেকোন বাস্তব সংখ্যা $y \,(y \ne 0)$ এর জন্য আমি লিখতে পারি, $y^{0} = 1$
অতএব $\displaystyle\lim_{y \to 0} y^{0} = 1$
তার মানে, $y$ এর মান যতই শূন্যের কাছে আনা হোক, $y^{0}$ মান $1$ কেই স্থির থাকে।
কাজেই আমরা দেখতে পাচ্ছি, $\text f(x,y)= y^x$ ফাংশনটি $(x,y)=(0,0)$ বিন্দুতে বিচ্ছিন্ন। আরো স্পষ্ট করে বললে, যদি আমরা $x=0$ সরলরেখা বরাবর $(0,0)$ বিন্দুর দিকে অগ্রসর হই, আমরা পাই
$\displaystyle\lim_{y \to 0}\text f(0,y) = 1$
কিন্তু আমরা যদি $y=0$ (যেখানে $x>0$) সরলরেখা বরাবর $(0,0)$ বিন্দুর দিকে অগ্রসর হই, তখন দেখি
$\displaystyle\lim_{x \to 0^{+}} f(x,0) = 0$
কাজেই, $\displaystyle\lim_{(x,y) \to (0,0)} y^{x}$ এর মান নির্ভর করবে আমরা কোন দিক থেকে লিমিট নিচ্ছি তার উপর। তার মানে হল $0^0$ কে সংজ্ঞায়িত করার এমন কোন উপায় নেই যা $y^x$ ফাংশনকে $(x,y) = (0,0)$ বিন্দুতে অবিচ্ছিন্ন করতে পারে।
গণিতবিদের বক্তব্য:
আমি বলছি, শূন্য টু দি পাওয়ার শূন্য এর মান হচ্ছে এক। কেন ? কারণ আমি গণিতবিদ এটা ঘোষণা করছি, তাই! আরে মজা করছি না, এটাই সত্য।

চলুন এই সমস্যাটিকে এই সমাধানের জন্য একটি ফাংশন $\text f(x,y) = y^x$ কে সংজ্ঞায়িত করি যেখানে, $x$ এবং $y$ উভয়ই ধনাত্বক পূর্ণসংখ্যা। এই ফাংশনকে বেশ কিছু পদ্ধতিতে সংজ্ঞায়িত করা যায়, যাদের সবগুলোই একই ফলাফল দেয়। উদাহরণ স্বরূপ একটা পদ্ধতি হচ্ছে,
এখানে, $y$ কে $x$ সংখ্যক বার পুনরাবৃত্তি করা হয়েছে। এ ক্ষেত্রে, যখন $x=1$ তখন $y$ কে একবার পুনরাবৃত্তি করা হয়, তাই লেখা যায়,
$y^{x}= y^1 = 1 \times y$
যা হোক, এই পদ্ধতিকে খুব সহজেই ধনাত্বক পূর্ণ সংখ্যা থেকে অঋণাত্বক পূর্ণ সংখ্যাতে বিস্তৃত করা যায়। তাই যখন $x$ শূন্য, তখন বলতে পারি $y$ কে শূন্য বার পুনরাবৃত্ত করা হল,
$y^{0} = 1$
যা যেকোন $y$ এর জন্য সত্য। তাই $y=0$ বসিয়ে আমরা পাই, $0^0 = 1$
দেখুন আমরা কিন্তু প্রমাণ করে ফেললাম, $0^0 = 1$ !
কিন্তু এটা $y^x$ কে সংজ্ঞায়িত করার শুধুমাত্র একটা সম্ভাব্য পদ্ধতি। তাহলে কী হত যদি আমি অন্যভাবে সংজ্ঞা দিতাম ? উদাহরণ স্বরূপঃ ধরুন, আমি $y^x$ কে এভাবে সংজ্ঞায়িত করলাম,
$y^x = \displaystyle\lim_{z \to x^{+}} y^{z}$
কথায় বলি, এটার মানে হচ্ছে, বাস্তব সংখ্যা $z$ ছোট হতে হতে $x$ এর নিকটবর্তী হতে থাকলে $y^z$ এর মান যা হয় সেটাই হয় $y^x$ এর মান।
[বিঃদ্রঃ আগ্রহী পাঠক জিজ্ঞেস করতে পারেন, $y^x$ কে সংজ্ঞায়িত করতে গিয়ে কিভাবে $y^z$ ব্যবহার করা সম্ভব ? এটা তো স্ববিরোধী মনে হচ্ছে ,তাই তো ?এটা ঠিক আছে কারণ আমরা এখানে শুধুমাত্র $z>0$ নিয়ে কাজ করছি। তাই এক্ষেত্রে $y^x$ সমান কত সে ব্যাপারে কেউ দ্বিমত পোষণ করবেন না আশা করি। মূলত আমরা চেনাজানা সহজ শর্ত ব্যবহার করেই একটা ফাংশন গঠন করতে যাচ্ছি যেন কঠিন শর্তে যেমনঃ $x=0$ ও $y=0$ তেও ফাংশনটির মান পাওয়া যাবে।]
চমৎকারভাবে, সংজ্ঞা ব্যবহার করে আমরা লিখতে পারি,
$\displaystyle 0^0 = \lim_{x \to 0^{+}} 0^{x} = \lim_{x \to 0^{+}} 0 = 0$
তাহলে আমরা $0^0=1$ এর বদলে $0^0=0$ পাচ্ছি। আমরা এই মাত্র যে সংজ্ঞাটি ব্যবহার করলাম সেটা অদ্ভুত অপ্রাকৃতিক মনে হতে পারে। কিন্তু এটা যেকোন বাস্তব ধনাত্বক সংখ্যা $x,\, y$ এর জন্য $y^x$ এর মান কেমন হবে সে সম্পর্কে সঠিক ধারণা দেয়। এবং সেই সাথে একটি নির্দিষ্ট সরলরেখা বরাবর $x=0$ ও $y=0$ এর দিকে অগ্রসর হলে দেখা যায় এটা ফাংশনের অবিছিন্নতা বজায় রাখছে।
তাহলে এই ব্যাখ্যা বা সংজ্ঞার মধ্যে কোনটা সঠিক ? $0^0$ এর সত্যিকার মান কত ? স্পষ্টভাবে, $x>0$ ও $y>0$ এর জন্য $y^x$ এর অর্থ কী তা আমরা জানি। কিন্তু যখন $x=0$ ও $y=0$ হয়, তখন এর কোন পরিষ্কার সুস্পষ্ট অর্থ থাকে না। দেখা যাচ্ছে, $y^x$ এর মান নির্ভর করে আমাদের পছন্দসই সংজ্ঞার উপর যেটা আমরা ঐ বিবৃতি দিয়ে বোঝাতে চাই। এবং ধনাত্বক মানের জন্য $y^x$ এর অর্থ সম্পর্কে আমাদের যা জ্ঞান তা শূন্য মানের জন্য সম্পূর্ণ ব্যাখ্যা দিতে যথেষ্ট নয়।
কিন্তু, তাই যদি হয়, তাহলে গণিতবিদেরা এত জোর গলায় কিভাবে বলছে, $0^0=1$ ?
আসলে এর নিছক কারণটা হল এই মান নিয়ে এটা বেশি ব্যবহার উপযোগী হয়। গণিতে খুবই গুরুত্বপূর্ণ কিছু সূত্র, নীতি অস্তিত্ব হারিয়ে ফেলবে যদি আমরা বলি $0^0$ মান শুন্য বা অসংজ্ঞায়িত। উদাহরণস্বরূপ, ধরুন একটা দ্বিপদী উপপাদ্য, যেটাতে বলা হলঃ
$\displaystyle (a+b)^x = \sum_{k=0}^{\infty} \binom{x}{k} a^k b^{x-k}$
যেখানে $\tbinom{x}{k}$ হচ্ছে দ্বিপদী সহগ।
এখন সমীকরণটির উভয় পাশে $a=0$ বসিয়ে $( b \ne 0)$ আমরা পাই,
$$\begin{align} b^x &= (0+b)^x \\ &= \sum_{k=0}^{\infty} \binom{x}{k} 0^k b^{x-k} \\ &= \binom{x}{0} 0^0 b^{x} + \binom{x}{1} 0^1 b^{x-1} + \binom{x}{2} 0^2 b^{x-2} + \cdots \\ &= \binom{x}{0} 0^0 b^{x} \\ &= 0^0 b^{x} \\ \end{align}$$
এখানে, আমি $\tbinom{x}{0} = 1$ এবং $k>0$ এর জন্য $0^k = 0$ ব্যবহার করেছি। দেখতে পাচ্ছেন, সমীকরণের ডানপক্ষে কিন্তু সেই জাদুকরী ফ্যাক্টর $0^0$ আছে। অর্থাৎ, আমরা এখানে যদি $0^0=1$ না ব্যবহার করতাম, তবে উপরে লেখা দ্বিপদী উপপাদ্যটি $a=0$ শর্তে ঠিক থাকত না। কারণ তখন $b^x$ তো আর $0^0 b^{x}$ এর সমান হত না।
যদি গণিতবিদদের $0^0 = 0$ ব্যবহার করতে হত, অথবা বলতে হত $0^0$ অসংজ্ঞায়িত, তবেও দ্বিপদী উপপাদ্য একই আকারে অব্যাহত থাকত, কিন্তু সেটা উপরে লেখা আকারের মত হত না। সেক্ষেত্রে উপপাদ্যটি খুব জটিল হয়ে পড়ত, কারণ এটাকে তখন $k=0$ সংশ্লিষ্ট বিশেষ শর্তগুলো নিয়ন্ত্রণ করতে হত। $0^0 = 1$ ব্যবহার করে আমরা এ বিষয়টিকে পরিষ্কার, মার্জিত ও সহজবোধ্য করতে পেরেছি।
$0^0 = 1$ এর ব্যবহার উপযোগীতা ও গ্রহণযোগ্যতার পেছনে আরো অনেক যৌক্তিক কারণ আছে। কয়েকটা এখানে দেখানো হলঃ
- যদি $\text p(x) = \displaystyle\sum_{n=0}^d a_n x^n$ একটা বহুপদী হয়, তবে $\text p(0) = a_0$ হচ্ছে তার ধ্রুবক পদ – কিন্তু আমরা কোন বহুপদী লিখতেই পারতাম না যতক্ষণ না $0^0 = 1$ হয়। সেই একই কারণে অসীম ঘাত ধারায় (infinite power series) $d$ কে $\infty$ দ্বারা প্রতিস্থাপিত করা হয়।
- অসীম জ্যামিতিক ধারার (infinite geometric series) বিশ্লেষণে,
$$\displaystyle{\begin{split} (1 – x) \sum_{n=0}^\infty x^n &= \sum_{n=0}^\infty x^n – x\sum_{n=0}^\infty x^n \\ &= \sum_{n=0}^\infty x^n – \sum_{n=0}^\infty x^{n + 1} \\ &= \sum_{n=0}^\infty x^n – \sum_{n=1}^\infty x^n \\ &= \sum_{n=0}^0 x^n \\ &= 1 \\ ∴ \sum_{n=0}^\infty x^n &= \frac{1}{1 – x} \end{split}}$$
এটা $x=0$ সহ $|x| < 1$ এর জন্য সম্পূর্ণভাবে বৈধ (এবং একইসাথে অবিচ্ছিন্ন), কিন্তু কেবল তখনই যখন $0^0 = 1$।
- $n = 1$ ও $x = 0$ হলেও অন্তরীকরণের power rule $\tfrac{d}{dx} x^n = nx^{n – 1},\, (n \ne 0)$ ঠিক থাকে, কিন্তু প্রয়োজন হয় $0^0 = 1$।
- ফাংশন $f \colon S \to T$ এর সংখ্যা $\lvert T\rvert^{\lvert S\rvert}$ হয়, কেবল যখন $0^0 = 1$ হয়।
গণিতে আরো অনেক প্রতিষ্ঠিত যুক্তি ব্যাপকভাবে ব্যবহৃত হয় যেসব কারণে $0^0=1$ এখন গ্রহণযোগ্য রূপ।
প্রাণবন্ত এই ভিডিওটি দেখে হাতে-কলমে $0^0 = 1$ উপভোগ করতে পারেনঃ
[youtube https://youtu.be/r0_mi8ngNnM&w=560&h=315&align=center]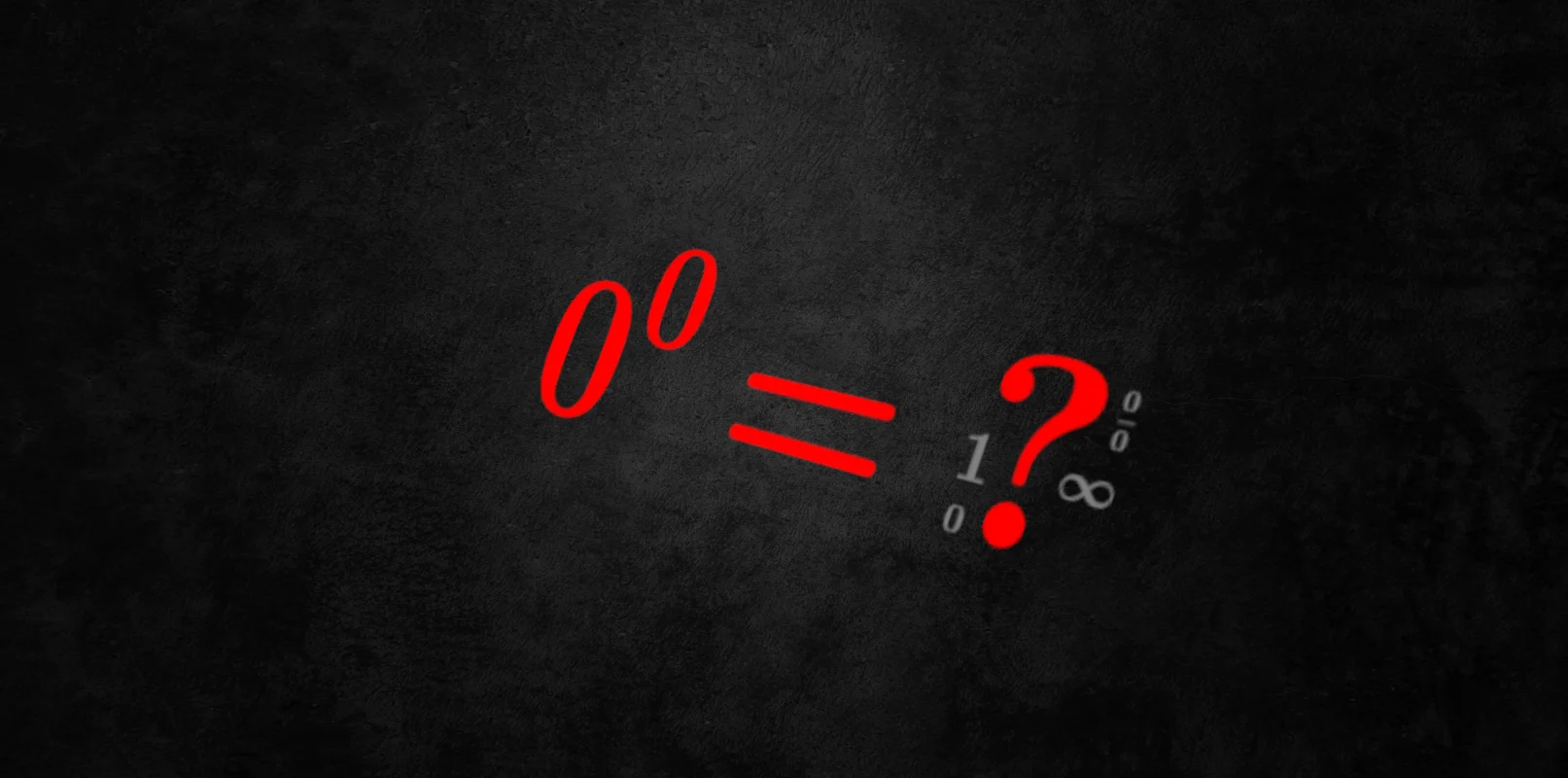





Leave a Reply