১.
রোনাল্ড রস তখন ব্রিটিশ আর্মির সার্জন হিসেবে ভারতের ব্যাঙ্গালোরে কাজ শুরু করেছেন। সব মিলিয়ে খুশিই ছিলেন। ইংল্যান্ডের রয়েল কলেজ অব সার্জন থেকে বের হয়েছেন মাত্র বছর-দুই হলো। তরুণ বয়সে ইচ্ছা ছিলো লেখক হবেন; কিন্তু তার বাবা লন্ডনের একটি মেডিকেল কলেজে পড়াশুনার ব্যবস্থা করে দেন। রস যে মেডিকেল কলেজে কঠোর পরিশ্রমে পড়াশুনা করতেন এমন না। তার অনেকটা সময় চলে যেত কবিতা লিখে, নাটক আর সঙ্গীত রচনা করে। সময়টা ১৮৮৩ সাল, পেশাগত জীবন মাত্র শুরু তখন। ব্যাঙ্গালোর বেশ পছন্দই হলো তাঁর। এখানকার রৌদ্রজ্বল দিন, বাগান আর ভিলা তার মতে দক্ষিণ ভারতের অন্যতম সুন্দর জায়গা। কিন্তু রোনাল্ড রস যখন মশার উপদ্রপে অতিষ্ট হয়ে তার বাংলোর বাইরে পানির ট্যাঙ্কি উপর করে দেন, তখন কি তিনি জানতেন মশাদের বিরুদ্ধে এটা তার জীবন-যুদ্ধ হতে যাচ্ছে? ব্যাঙ্গালোরে পৌঁছে রস দেখলেন তার ঘর মশাদের গুঞ্জনের শব্দে ভরে আছে। তখন ঠিক করলেন মশাদের সংখ্যা কমাতে হবে, এদের আর প্রজনন করতে দেয়া যাবে না। তাই বাংলোর আশেপাশে যেখানে যেখানে বদ্ধ পানি জমে থাকতে দেখলেন সেখানকার পানি সরিয়ে দিলেন। এ পদ্ধতি কাজ করলো — কমে গেল মশকীর সংখ্যা।
ঐ অঞ্চলে দিনযাপনের সাথে সাথে রোনাল্ড রস ক্রমেই একটা ধারণা বদ্ধমত হতে থাকেন যে সেখানকার মশারা সম্ভবত ম্যালেরিয়া রোগ ছড়াচ্ছে। ম্যালেরিয়া একটা প্রাণঘাতী রোগ। প্রচন্ড জ্বরের সাথে সাথে ফ্লু-এর বিভিন্ন লক্ষণ সাথে নিয়ে হাজির হয় এই রোগটি। বর্তমান মানব প্রজাতী, Homo sapiens-এর উদ্ভবের প্রায় শুরু থেকেই এই রোগটি ছিলো। পূর্বে ধারণা ছিলো কোন খারাপ-বাতাসের সংস্পর্শে আসলে মানুষের এই রোগটি হয়। ম্যালারিয়া শব্দটা এসেছেই ইতালিয়ান ভাষার ম্যাল-এরিয়া, থেকে যার অর্থ খারাপ-বাতাস।

মশা ও ম্যালেরিয়া রোগের মধ্যকার সম্পর্ক প্রমাণের জন্য রোনাল্ড রস পাখি নিয়ে পরীক্ষা-নিরীক্ষা করা শুরু করেন। তিনি ম্যালেরিয়া আক্রান্ত পাখিকে মশা কামড়ানোর ব্যবস্থা করেন। তারপর ওই মশাদের সুস্থ পাখির রক্ত চোষার ব্যবস্থা করেন। দেখা গেল কিছু দিনের মধ্যেই সুস্থ পাখিগুলোও ম্যালেরিয়ায় আক্রান্ত হয়ে গেছে। তার এই মশকী-তত্ত্ব যাচাই করে দেখার জন্য রস এই মশকীগুলোর ব্যবচ্ছেদ করেন। এই মশকীগুলোর লালাগ্রন্থিতে ম্যালেরিয়ার জীবাণু খুঁজে পান তিনি। পরবর্তীতে একজন ফরাসি মিলিটারী ডাক্তার এই জীবাণুকে প্লাজমোডিয়াম (Plasmodium) হিসেবে সনাক্ত করেন। সেই ফরাসী ডাক্তার মাত্র কয়েক বছর আগেই ম্যালেরিয়া আক্রান্ত রোগীর রক্তকোষে এই জীবাণু আবিষ্কার করেছিলেন।
ম্যালেরিয়া রোগ বিস্তার কিভাবে থামানো যায় তা রোনাল্ড রসের গবেষণার পরবর্তী আগ্রহ হয়ে দাঁড়ায়। ব্যাঙালোর জীবনে প্রবেশ করার সময় বদ্ধ ট্যাঙ্কি থেকে পানি ফেলে দেয়ার পদ্ধতিটা এ সময় আবারো উপযুক্ত মনে হয় তার কাছে। তিনি প্রস্তাব করেন, মশকীর সংখ্যা যথেষ্ট পরিমাণে কমাতে পারলে ম্যালেরিয়ার বিস্তার এমনিতেই কমে আসবে। ছাত্রজীবনে গণিত-প্রেমী রোনাল্ড রস তার এই তত্ত্ব প্রমাণের জন্য এবার তার গণিতজ্ঞান কাজে লাগালেন। তিনি একটি গাণিতিক মডেল তৈরি করলেন – যাকে বলা যায় মশকী তত্ত্ব। এই মশকী তত্ত্ব গাণিতিকভাবে ব্যাখ্যা করলো কিভাবে একটি নির্দিষ্ট মানব জনপুঞ্জে (human population) মশকী ম্যালেরিয়া ছড়াতে পারে। তিনি সেই মডেলে মানব জনপুঞ্জকে দু’ভাগে বিভক্ত করেন – একদলে রইলো সুস্থ, অন্যদলে আক্রান্ত। তারপর তিনি বেশ কিছু গাণিতিক সমীকরণ লিখে ফেললেন যারা ব্যাখ্যা করে যে মশার সংখ্যা কিভাবে এই রোগের বিস্তারকে প্রভাবিত করতে পারে।
ম্যালেরিয়ার জীবাণু প্লাজমোডিয়াম হলো পরজীবী। প্লাজমোডিয়ামের জীবনচক্র সম্পূর্ণ করার জন্য ওর মানুষ ও মশা দুই বাহকেরই প্রয়োজন হয়। দেখা যায় কারো ম্যালেরিয়ায় আক্রান্ত হওয়ার হারের সঙ্গে তিনি কতবার প্লাজমোডিয়াম-বাহক মশার কামড় খেয়েছেন তার একটা সম্পর্ক আছে। প্লাজমোডিয়াম-বাহক মশার সাথে আবার সম্পর্ক রয়েছে কতজন ম্যালেরিয়া আক্রান্ত রোগীর রক্তে প্লাজমোডিয়াম কীট রয়েছে। অ্যানোফিলিস মশা ম্যালেরিয়া আক্রান্ত রোগীর রক্তে প্লাজমোডিয়াম কীট উপস্থিত থাকা অবস্থায় রোগীর রক্ত চুষে ফেললে একটি সাধারণ মশা প্লাজমোডিয়ামে আক্রান্ত হয়ে যাবে। এই সম্পর্কগুলোকেই রোনাল্ড রস গাণিতিক ভাবে ব্যাখ্যা করেন। তিনি দেখলেন ভারতের মতো জায়গায় ম্যালেরিয়ার সংক্রমণ স্থায়ীভাবে ঘটতে হলে সেখানে প্রতি মাসে কত জন নতুন করে ম্যালেরিয়ায় আক্রান্ত হবে তা অবশ্যই ঐ মাসে কতজন রোগী ম্যালেরিয়া থেকে সুস্থ হয়ে উঠছে তার সমান হতে হবে।
এই গাণিতিক মডেলটি ব্যবহার করে রস দেখালেন ম্যালেরিয়া নিয়ন্ত্রণের জন্য সব মশা মেরে ফেলার কোন দরকার নেই। যথেষ্ট পরিমাণ মশা মেরে ফেলো, তাহলে ম্যালেরিয়ায় আক্রান্ত রোগী যথেষ্ট পরিমাণ মশা কামড়ানোর আগেই সে সেরে উঠবে। ফলে রোগসংক্রামণের হারও আর আগের মতো থাকবে না। ফলশ্রুতিতে ম্যালেরিয়া রোগের বিস্তার কমে আসা শুরু করবে। অন্যভাবে বলা যায় সংক্রামণের একটা নির্দিষ্ট পরিমাণ আছে — এ পরিমাণের চেয়ে বেশি সংক্রামণ হলে তা মহামারীতে পরিণত হবে আর কম হলে রোগটি আপনা আপনিই কমে যাবে।
রসের এই কাজ ১৯০২ সালে তাকে চিকিৎসাশাস্ত্রে নোবেল এনে দেয়। বিভিন্ন রোগের বিস্তার ও মহামারীকে যে গাণিতিক ভাবে বিশ্লেষণ করা সম্ভব সেই সম্ভাবনার ভিত্তিরোপন করে রসের এই কাজটি। রোনাল্ড রসের এই অন্তর্দৃষ্টি ভ্যাক্সিন প্রয়োগের নীতিকেও প্রভাবিত করে দলীয়-অনাক্রম্যতা বা দলীয়-রোগ-প্রতিরোধ-ব্যবস্থার (Herd Immunity) ধারণার মাধ্যমে। দলীয়-অনাক্রম্যতার মূল ধারণা হলো একটি জনপুঞ্জে যথেষ্ট সংখ্যক মানুষকে কোন রোগের টীকা দিয়ে দাও; তাতে ওই রোগ বিস্তার কমে যাবে আপনাআপনিই। তার মানে টীকা দেয়া কর্মসূচী থেকে কিছু মানুষ বাদ গেলেও সে কর্মসূচী সফলভাবে কাজ করতে পারে। যদিও টীকা দেয়ার থেকে রোনাল্ড রসের কর্মসূচী ভিন্ন ছিলো – রস টীকা দেন নি; তিনি মশার পরিমাণ কমানোর ব্যবস্থা করেছেন। কিন্তু তবুও উভয়ক্ষেত্রে মূলনীতিটা একই। কোন জনপুঞ্জে সকলকে টীকা দেয়ার দরকার নেই বা সকল মশা সরানোর দরকার নেই। প্রয়োজন একটি নির্দিষ্ট সংকট সীমায় (critical threshold) পৌঁছানো। যদি সে সীমায় পৌঁছানো যায় তাহলে ওই রোগটি সহজে আর ছড়াতে পারবে না।
রোনাল্ড রসের হাত ধরে গাণিতিক রোগতত্ত্ববিদ্যার যে পথচলা শুরু হয়েছিলো তা বহুদূর এগিয়েছে পরের একশ-বছরে। আমরা এখন ঘুরে আসবো মহামারীর গাণিতিক বিশ্লেষণের কিছু ইতিহাস থেকে।
২.
রোনাল্ড রসের আগেও বিজ্ঞানীরা রোগব্যাধি বিষয়ক গবেষণায় গণিতকে প্রয়োগ করেছিলেন। তবে তাদের গবেষণার বিষয়বস্তু ছিল অতীতের ঘটনা। যেমন জন স্নো নামের একজন চিকিৎসক ১৮৫৪ সালে লন্ডনে কলেরা রোগের প্রাদুর্ভাবের কারণ খোঁজার জন্যে যুক্তিবিদ্যার সহায়তা নিয়েছিলেন। তখন অধিকাংশ মানুষ ম্যালেরিয়ার মতো কলেরাও “খারাপ বাতাস”-এর প্রভাবে হয়ে থাকে বলে মনে করতেন। কলেরা কোন কোন স্থানে ঘটেছিলো জন স্নো সেটা ম্যাপে চিহ্নিত করা শুরু করেন। তখন তিনি খেয়াল করলেন লন্ডনের সোহো পাড়ার পানির পাম্প থেকে কলেরা আক্রান্ত বাড়িগুলোতে পানি সরবরাহ করা হয়। তিনি যুক্তি দিলেন যে রোগীরা কলেরা আক্রান্ত হচ্ছে দূষিত পানি থেকে আর বোর্ড স্ট্রিটের ওই পানির উৎস সরিয়ে ফললে কলেরার বিস্তার থেমে পড়বে।
বিপরীতে অতীতের মহামারীর দিকে না তাকিয়ে রোনাল্ড রস দেখলেন ভবিষ্যতের দিকে। মহামারী কিংবা রোগ বিস্তারের গতিপথ ভবিষ্যদ্বাণী করার জন্যে তার উদ্দীপনার মাধ্যমে প্রভাবিত হলেন অন্যান্য সহকর্মীরা। এন্ডারসন ম্যাককেন্ড্রিক নামের একজন তরুণ স্কটিশ গণিতবিদ রসের সাথে দেখা করেছিলেন সিয়েরা লিয়নের একটি ম্যালেরিয়া প্রতিরোধ কার্যক্রমে। ম্যাককেন্ড্রিক তখন ভারতীয় মেডিক্যাল সার্ভিসের একজন সদস্য হিসেবে কাজ করছিলেন। তবে ১৯২০ সালে পেটের পীড়ায় আক্রান্ত হয়ে তিনি ভারত ছেড়ে ফিরে যান স্কটলান্ডে। রাজধানী এডিনবার্গে তিনি রয়েল কলেজ অব ফিজিশিয়ান-এর গবেষণাগারে সুপারইন্ডেন্ট হিসেবে যোগ দেন। সেখানে ম্যাককেন্ড্রিকের কথা হয় সংক্রামক রোগ বিষয়ে আগ্রহী রসায়নবিদ উইলিয়াম কারম্যাকের সাথে।
প্লেগের মতো রোগের সাথে ম্যালেরিয়ার মতো রোগের পার্থক্য হল ম্যালেরিয়া-মহামারী একটি জনপুঞ্জে সবসময় টিকে থাকতে পারে। আর প্লেগের মতো রোগ একটি জনপুঞ্জ থেকে নিঃশেষ হয়ে যাওয়ার আগে বিস্ফোরণের মতো ছড়িয়ে পড়ে। রোনাল্ড রস মহামারীর গতিপ্রকৃতি বোঝার জন্য যে পদ্ধতি ব্যবহার করেছিলেন, সে পদ্ধতিকে আরও সামনে এগিয়ে নেয়ার জন্য ম্যাককেন্ড্রিক ও কারম্যাক কাজ শুরু করেন। ম্যালেরিয়ার মতো রোগের পাশাপাশি তারা প্লেগের মতো বিস্ফোরিত হয়ে হারিয়ে যাওয়া মহামারী নিয়েও গবেষণা করতে থাকেন।
একটি কাল্পনিক জনপুঞ্জের সদস্যদের তারা রসের মতো স্বাস্থ্যবান কিংবা রোগাক্রান্ত এই দুইটি দলে বিভক্ত করেন। তবে এক্ষেত্রে মশা জীবাণুর মধ্যবর্তী-বাহক নয়, বরং মানুষ থেকে সরাসরি মানুষেই রোগটি সংক্রমিত হচ্ছে। আগের মতোই জনপুঞ্জের সদস্যরা শুরুর দিকে রোগের প্রতি সংবেদনশীল থাকে। জীবাণুর সংস্পর্শে এসে তারা সুস্থ দল থেকে রোগাক্রান্ত দলে স্থান্তান্তরিত হয়। শেষে হয়তো তারা রোগাক্রান্ত দল থেকে আবার সুস্থ দলে ফিরে আসে (তাদের দেহ ঐ রোগের বিরুদ্ধে অনাক্রম্যতা গড়ে তোলে। যেমনটা হয় হাম কিংবা বিভিন্ন দেশে ছড়িয়ে পড়া ইনফ্লুয়েঞ্জার ক্ষেত্রে) কিংবা রোগে ভুগে মারা যায় (যেমনটা হয় প্লেগের ক্ষেত্রে)।
গবেষণায় অগ্রগতির সব সময় মসৃণ পথে হয় না। ১৯২৪ সালে ল্যাবের এক দুর্ঘটনায় কারম্যাক অন্ধ হয়ে পড়েন। তবু তিনি হতাশ না হয়ে মাথার মধ্যেই দরকারি হিসেব কষা শুরু করেন। তিনি ও ম্যাককেন্ড্রিক দুজনে মিলে গবেষণার ফলাফল ১৯২৭ সালে একটি গবেষণাপত্র লন্ডনের রয়েল সোসাইটির প্রসেডিংসে প্রকাশ করেন। গবেষণাপত্রের শিরোনাম ছিল ‘A Contribution to the Mathematical Theory of Epidemics’। বিশ পৃষ্ঠার এই গবেষণাপত্রে তারা রোগতত্ত্বের অন্যতম গুরুত্বপূর্ণ প্রশ্নের ব্যাখ্যা দেয়ার চেষ্টা করেন। প্রশ্নটি হল ঠিক কি কারণে কোন মহামারীর অবসান হয়?
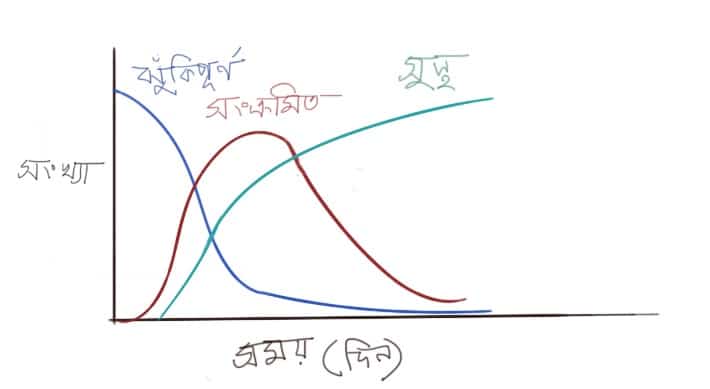
ইনফ্লুয়েঞ্জা কিংবা প্লেগ – যেকোনো মহামারীর শুরুতে রোগাক্রান্ত রোগীর সংখ্যা সাধারণত সূচকীয় হারে বাড়তে থাকে। কিছু সময় পর মহামারী একটি সর্বোচ্চ সীমার চূড়ায় পৌঁছে যায়। তারপর ঐ মহামারীতে রোগাক্রান্ত রোগীর সংখ্যা কমতে শুরু করে। ম্যাককেন্ড্রিক ও কারম্যাক যখন তাদের গবেষণা শুরু করেন তখন সমকালীন বিজ্ঞানী মহলে এই কমে যাওয়ার দুইটি ব্যাখ্যা প্রচলিত ছিল। হয়তো জীবাণুর ক্ষমতা সময়ের সাথে কমে এসেছে; কিংবা ঐ রোগের প্রতি সংবেদনশীল মানুষ ঐ জনপুঞ্জে আর নেই। ঐ জনপুঞ্জের সকলেই রোগাক্রান্ত হয়েছিলো – প্রত্যেকে হয় মারা গেছে কিংবা ঐ রোগের বিরুদ্ধে অনাক্রম্যতা অর্জন করে ফেলেছে।

ম্যাককেন্ড্রিক ও কারম্যাক তাদের মডেলে ধরে নিলেন যে সময়ের সাথে মহামারীর জীবাণু দুর্বল হয়ে যায় নি – আগের মতোই শক্তিশালী আছে। তারপরও তাদের গণিতে দেখা গেলো এক সময় ঠিকই রোগাক্রান্তের সংখ্যা কমে আসছে। যখন বিজ্ঞানী-যুগল ভারতের বোম্বে শহরে (এখনকার মুম্বাই) ১৯০৫ সালে প্লেগ মহামারীর তথ্য নিয়ে কাজ করলেন দেখা গেলো তাদের মডেল বিভিন্ন সময়ে রোগাক্রান্তের যে সংখ্যা হিসেব করছে তা প্রকৃত রোগীর সংখ্যার সাথে মিলে যাচ্ছে।
তাহলে কি মহামারীর এই কমতি রোগের প্রতি সংবেদনশীল মানুষের অভাবেই ঘটছে? আপাতদৃষ্টিতে না। ম্যাককেন্ড্রিক ও কারম্যাকের মডেল অনুসারে মহামারীর শেষ পর্যায়েও বেশ কিছু সংবেদনশীল ব্যক্তি বাকি রয়ে যান। তারা দেখান যে মহামারীর শেষ দিকে রোগীর সংখ্যা কমে আসার কারণ এই নয় যে জনপুঞ্জের সকলেই রোগাক্রান্ত হয়েছে। রোগীর সংখ্যা কমার আরেকটি কারণ হল ওই জনপুঞ্জে রোগসংক্রমণ জিইয়ে রাখার মতো যথেষ্ট সংখ্যক রোগাক্রান্ত ব্যক্তি থাকে না। যখন কোন জনপুঞ্জে যথেষ্ট সংখ্যক সদস্য রোগের বিরুদ্ধে প্রতিরোধ ক্ষমতা অর্জন করে ফেলেছে তখন রোগাক্রান্ত ব্যক্তিরা আরেকজন সংবেদনশীল সদস্যের সাথে সংস্পর্শে আসবে সেই সম্ভাব্যনা কমে আসে। অর্থাৎ তখন রোগাক্রান্ত ব্যক্তি হতে অন্য ব্যক্তিদের দেহে রোগ ছড়িয়ে পড়ার পূর্বেই রোগীরা সুস্থ হয়ে উঠছেন।
প্রাকৃতিক ভাবে কোন মহামারীর শেষ দিকে এই পরিণতি অনিবার্য। তবে অন্যভাবেও মহামারীকে এ অবস্থায় চলে যেতে বাধ্য করা যেতে পারে। রসের মডেল অনুযায়ী ম্যালেরিয়া সংক্রমণ কমানো হয়েছিলো মশার সংখ্যা কমিয়ে। আর টিকা দান কর্মসূচীতে জনপুঞ্জে রোগের প্রতি সংবেদনশীল একটি বড় অংশকে টিকা দিয়ে রোগ ছড়ানো বন্ধ করা হয় (কিংবা নিয়ন্ত্রণে নিয়ে আসা হয়)।
ম্যাককেন্ড্রিক ও কারম্যাকের মডেলের পরে বড় ধরনের মৌলিক আবিষ্কারের জন্য রোগতত্ত্বকে অপেক্ষা করতে হয় আরো কয়েকটি দশক। ১৯৭০-এর দশকে গণিতবিদ ক্লাউস ডিয়েট্জ এবং দুই বাস্তুবিদ (ecologist) রয় এন্ডারসন ও রবার্ট মে ‘পুনরুৎপাদন সংখ্যা’ বা reproduction number ধারণার উপর তাদের অগ্রণী গবেষণা শুরু করেন। রোগতত্ত্বে পুনরুৎপাদন সংখ্যা বলতে বোঝায় কোন রোগে আক্রান্ত ব্যক্তি রোগে ভোগা অবস্থায় গড়ে নতুন কয়জন সুস্থ ব্যক্তিকে আক্রান্ত করতে পারে। একটি রোগের ছড়িয়ে পড়ার ক্ষেত্রে অনেক ধরনের প্রক্রিয়া ভূমিকা পালন করে – রোগীর সামাজিক মেলামেশা থেকে শুরু করে জীবাণুর আক্রমণ করার জৈবিক ক্ষমতা সহ অনেক কিছুই। পুনরুৎপাদন সংখ্যার মাধ্যমে এসব প্রক্রিয়াকে একটি মাত্র পরিমাপে নিয়ে আসা যায়। যদি পুনরুৎপাদন সংখ্যা ১-এর চাইতে ছোট হয়, প্রতিটি রোগীর মাধ্যমে গড়ে ১-এর চেয়ে কম নতুন কোন সুস্থ ব্যক্তিকে আক্রান্ত করবে ঐ জীবাণু। সেক্ষেত্র কোন বড় আকারে ছড়িয়ে না পড়ে রোগটি জনপুঞ্জ থেকে চলে যাবে। কিন্তু এই সংখ্যাটা যদি ১-এর চেয়ে বেশি হয় তাহলে সময়ের সাথে সাথে জনপুঞ্জে রোগটি ছড়িয়ে পড়তে থাকবে।
কোন রোগের পুনরুৎপাদন সংখ্যা অনেকভাবেই গোনা যায়। যদি জানা থাকে একটি রোগে আক্রান্ত ব্যক্তি কত দিনের মধ্যে অন্য সুস্থ ব্যক্তিদের আক্রান্ত করতে পারে – আর যদি জানা থাকে একটি নতুন রোগের ঘটনা থেকে অন্য একটি রোগ সংক্রমণের মধ্যে গড় সময় পার্থক্য – তাহলে কত দ্রুত মহামারী বেড়ে উঠছে তা থেকে পুনরুৎপাদন সংখ্যা আমরা বের করতে পারবো। কিংবা কোন রোগে মানুষ গড়ে কত বছর বয়সে আক্রান্ত হয় সেটা জানা থাকলেও পুনরুৎপাদন সংখ্যা বের করা যায়। একটি রোগ যত বেশি সংক্রামক হবে তত দ্রুত কোন ব্যক্তি রোগাক্রান্ত হবে।
বিভিন্ন রোগের পুনরুৎপাদন সংখ্যা তুলনা করে বিভিন্ন রোগের ভয়াবহতা সম্পর্কে একটি ধারণা পাওয়া যায়। যেমন হাম খুবই সংক্রামক রোগ। টিকা দেয়া হয় নি এমন জনপুঞ্জে এর পুনরুৎপাদন সংখ্যা ১২ থেকে ১৮ হতে পারে। এ থেকে বোঝা যায় যে কেন হামকে ছোটদের রোগ হিসেবে ধরা হয়। অন্যদিকে কুখ্যাত স্প্যানিশ ফ্লু-র পুনরুৎপাদন সংখ্যা ২ থেকে ৩-র মাঝামাঝি। ১৯১৮/১৯ সালে স্প্যানিশ ইনফ্লুয়েঞ্জা পৃথিবীর এক-তৃতীয়াংশ মানুষকে আক্রান্ত করেছিলো। মারা গিয়েছিলো তখনকার পৃথিবীর ৩ থেকে ৫ শতাংশ অধিবাসী। এ রোগে মৃত্যুর হার বেশি বলে তুলনামূলক কম পুনরুৎপাদন সংখ্যা হলেও তা পৃথিবী জুড়ে একটা ধ্বংসযজ্ঞ ছড়াতে পেরেছিল। পুনরুৎপাদন সংখ্যার স্কেলে মাঝামাঝি আছে পোলিও (৫ থেকে ৭) ও মাম্পস (৪ থেকে ৭)।
একটি রোগ কত দ্রুত ছড়াবে সে সম্পর্কে পুনরুৎপাদন সংখ্যা কোন তথ্য দেয় না। তবে টিকা দান কর্মসূচীর মাধ্যমে কোন রোগকে নির্মূল করে ফেলতে কি পরিমাণ প্রচেষ্টা চালানো লাগবে তার একটা ধারণা পাওয়া যায়। যেমন হামের মতো রোগের ক্ষেত্রে জনপুঞ্জের ভালো পরিমাণ সদস্যকে টিকা দিতে হবে যাতে প্রাথমিক রোগী থেকে হাম তেমন একটা না ছড়ায়, যাতে পুনরুৎপাদন সংখ্যা ১-র নিচে চলে আসে। এমন নয় পুনরুৎপাদন সংখ্যা কেবল চেনা-পরিচিত রোগের ক্ষেত্রেই সহায়ক। ইবোলার মতো নতুন রোগ কিভাবে মোকাবেলা করতে হবে সেক্ষেত্রেও এ সংখ্যাটি আমাদের সাহায্য করে।
এডাম কোচারাস্কি লন্ডন স্কুল অব হাইজিন এন্ড ট্রপিক্যাল মেডিসিনে গবেষণা ফেলো। Aeon-এ প্রকাশিত The calculus of contagion লেখাটির অনুবাদ। অনুবাদটি আমার বই প্রাণের বিজ্ঞান: সাম্প্রতিক জীববিজ্ঞানের ভাবনা ভাষান্তর (২০১৭) থেকে নেয়া।
Leave a Reply