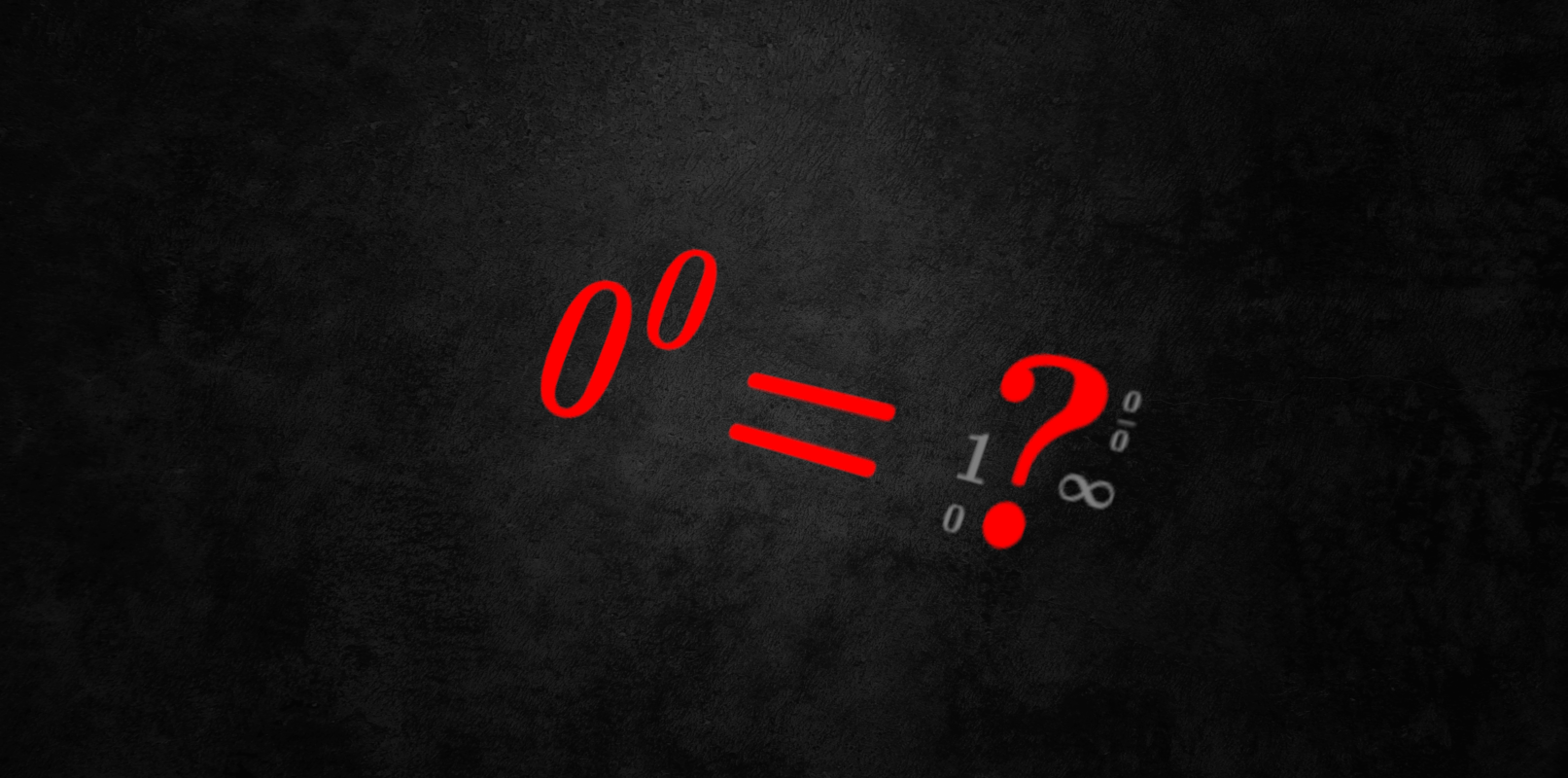গণিত
%22%20transform%3D%22translate(1.9%201.9)%20scale(3.76563)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23fff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-1.42264%20-41.67795%20210.87719%20-7.19811%2097.5%20244.6)%22%2F%3E%3Cellipse%20fill%3D%22%2383420c%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(42.73661%2067.57673%20-178.33073%20112.77922%2078.5%2048.5)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20cx%3D%22145%22%20cy%3D%22249%22%20rx%3D%22170%22%20ry%3D%2233%22%2F%3E%3Cellipse%20fill%3D%22%23244c50%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(18.12122%2029.68732%20-44.09582%2026.9162%2016.5%20138.6)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
দাবা আবিষ্কারক ও করোনা (অনুজীবের) মহামারী!
উপরোক্ত টাইটেল দেখেই ঘাবড়ে যাবার কিছুই নেই। স্বভাবতই প্রথমে অনেকেরই মনে হবে, কি উদ্ভট কথাবার্তা। একটা হচ্ছে গণিত (নন-বায়োলজি) সম্পর্কিত আরেকটি হচ্ছে বায়োলজি। আমি করোনা (কিংবা যে সকল অণুজীব) যা কিনা ব্যক্তির সংস্পর্শে ছড়ায় তার সঙ্গে একটু দাবা আবিষ্কারকের ঘটনার সম্পৃক্ত করতে চাই। এর জন্যে প্রথমে আমাদের “দাবা-আবিষ্কারের” মজার ঘটানাটি জানা দরকার। দাবা আবিষ্কারের গল্পটা…
%22%20transform%3D%22translate(.5%20.5)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23ff8e4b%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(134.7%20-3.5%2035.6)%20scale(31.93705%2044.18807)%22%2F%3E%3Cellipse%20fill%3D%22%23004f3e%22%20cx%3D%22130%22%20cy%3D%2241%22%20rx%3D%2235%22%20ry%3D%22149%22%2F%3E%3Cpath%20fill%3D%22%23715f6d%22%20d%3D%22M61%2070l59-23.6-2.2-35.2-67.2%2024.3z%22%2F%3E%3Cellipse%20fill%3D%22%23133738%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(4.9725%2021.20036%20-38.28438%208.97952%2070.6%203.3)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
শূন্যের ওপারে
আমাদের ছোট্টবেলার জ্ঞান থেকে শুরু করি। কোন কিছু নেই মানে ‘শূন্য’। কোন কিছুর অবস্থান নেই, খালি, ফাপা বোঝাতে যে সংখ্যাটি আমরা ব্যবহার করি তা হলো শূন্য। আমরা দৈনন্দিন কাজে যে দশ ভিত্তিক সংখ্যা ব্যবস্থা ব্যবহার করি, তার প্রথম অঙ্কটি শূন্য। এছাড়াও বাইনারী, ট্রাইনারী সহ প্রায় পরিচিত সকল ধরণের সংখ্যাব্যবস্থা শুরু হয় শূন্য দিয়ে। বইয়ের ভাষায়…
%22%20transform%3D%22translate(1.6%201.6)%20scale(3.125)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%235f1f74%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(6.94645%2015.93339%20-26.13884%2011.3957%20127.3%20111.9)%22%2F%3E%3Cellipse%20fill%3D%22%23001747%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-12.769%203.75876%20-9.25267%20-31.43256%20110.8%2073.6)%22%2F%3E%3Cellipse%20fill%3D%22%23002753%22%20cx%3D%22106%22%20cy%3D%2259%22%20rx%3D%2217%22%20ry%3D%2217%22%2F%3E%3Cpath%20fill%3D%22%2346357a%22%20d%3D%22M101%20133l3-39%2040%2034z%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
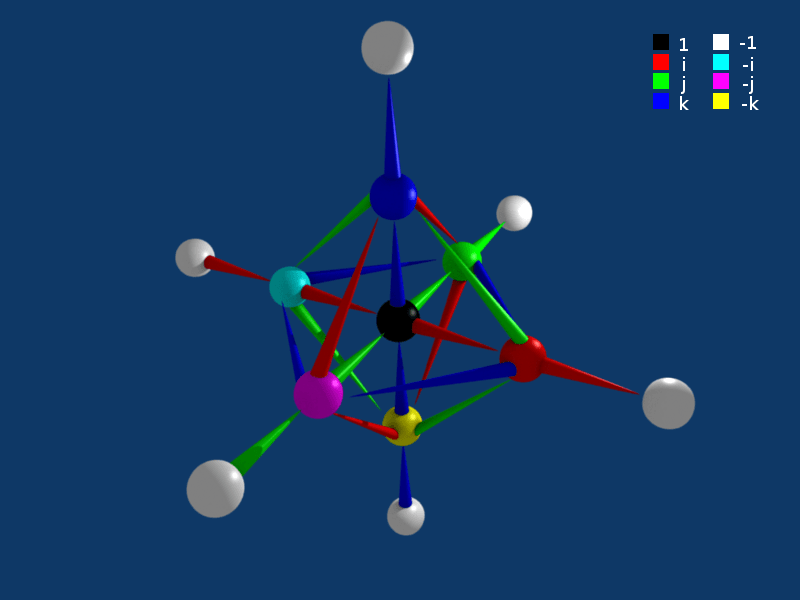
কোয়াটারনিয়ন: সংখ্যার এক অন্যভুবন
ঘড়ির ঘণ্টার কাটা ঘুরানোর কথা চিন্তা করুন। গণিতবিদেরা অনেক আগে থেকেই জানেন কিভাবে এধরনের ঘূর্ণনকে সাধারণ গুণন দিয়ে ব্যাখ্যা করা যায়। খুব সহজ, যে সংখ্যা দিয়ে কাটার অবস্থান প্রকাশ করা হল, সেটাকে আরেকটা ধ্রুবক সংখ্যা দিয়ে গুণ করলে ঘুরে যাবে অবস্থান। এ ঘুর্ণন তো ছিল একটা তলে, মানে দ্বিমাত্রিক ঘুর্ণন। তাহলে এরকম সহজ উপায় দিয়ে…
%22%20transform%3D%22translate(1.6%201.6)%20scale(3.125)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23fff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-254.02965%20-22.22471%202.21915%20-25.36505%20150.4%2014.6)%22%2F%3E%3Cellipse%20fill%3D%22%23d7d7d7%22%20cx%3D%22133%22%20cy%3D%2274%22%20rx%3D%2256%22%20ry%3D%2256%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-18.94668%20-20.06451%2065.03097%20-61.40797%2047.3%200)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-21.98897%2024.68376%20-103.62839%20-92.31498%20241.6%2040)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
অসীম ধারার গল্প
নবম দশম শ্রেণীতে আমাদের অসীম ধারার সাথে পরিচয় ঘটে। বিশেষ করে গুণোত্তর ধারার সাথে পরিচয় হওয়ার দিন কয়েক পরেই আমরা শিখি যে ,$$ \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdots \cdots = 1$$ সাধারণভাবে এটা আমরা গাণিতিকভাবে মেনে নেই, কিন্তু কেনো অসীম পর্যন্ত নিয়ে সমষ্টি $1$ পাওয়া যায়, তা বোঝার চেষ্টাও করি না।দেখা যাক আমরা…
%27%20fill-opacity%3D%27.5%27%3E%3Cellipse%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(133.8025%20-86.89237%2020.58381%2031.69629%20251.5%20226.2)%22%2F%3E%3Cellipse%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(26.42471%20-33.83335%20152.21995%20118.88768%2042%20236.1)%22%2F%3E%3Cellipse%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(16.2088%20-28.41704%20153.90647%2087.7867%20274%2020.8)%22%2F%3E%3Cellipse%20fill%3D%22%23777%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-146.38567%20.51098%20-.2917%20-83.56551%20156.4%20114.7)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
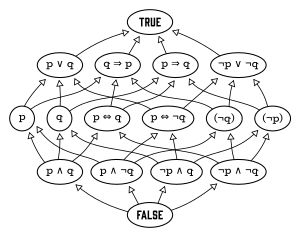
বুলিয়ান বীজগণিতের গোড়ার কথা
অনেকেরই বুলিয়ান অ্যালজেব্রা নিয়ে বুঝতে সমস্যা হয়। বুলিয়ান অ্যালজেব্রায় এক আর একে কিভাবে এক হয় সে রহস্যের পর্দা উন্মোচন করতে হলে আমাদেরকে বুলিয়ান অ্যালজেব্রার একেবারে গোড়ায় যেতে হবে।প্রথমে নিচের কয়েকটা উদাহরণ দেখা যাকঃউদাহরণ-১আগামীকাল হয় বৃষ্টি হবে অথবা তুষারপাত হবে।এখন এত গরম যে আগামীকাল তুষারপাত হবে না।সুতরাং, আগামীকাল বৃষ্টি হবে।উদাহরণ-২যদি আজকে শুক্রবার হয় তবে আমাকে স্কুল…
%22%20transform%3D%22translate(3.2%203.2)%20scale(6.30078)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%232f2f2f%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-9.31827%20-88.00188%2069.72295%20-7.38277%20117.3%2041)%22%2F%3E%3Cellipse%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-21.74105%20206.52833%20-51.38098%20-5.40883%20235.2%2067.2)%22%2F%3E%3Cellipse%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(39.17133%20226.7778%20-31.20514%205.39006%2029.3%20117.3)%22%2F%3E%3Cellipse%20cx%3D%22221%22%20cy%3D%2262%22%20rx%3D%2235%22%20ry%3D%22255%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
0 এর 0 তম সূচক কত?
১৯ শতকের প্রথমদিকেও গণিতবিদদের মহলে শূন্যের শূন্যতম ঘাত বা সূচক $(0^0)$ এর ব্যাখ্যা একটি বিতর্কের বিষয় ছিল। সেসময়কার অধিকাংশ গণিতবিদেরা মেনে নিয়েছিলেন $0^0=1$। কিন্তু সমস্যা বেধেছিল, ১৮২১ সালে গণিতবিদ Cauchy $0^0$ কে $\frac{0}{0}$ এর মত অনির্ণেয় আকারগুলোর সাথে একই তালিকাভুক্ত করলেন। আবার ১৮৩০ এর দশকে গণিতবিদ Libri $0^0=1$ এর পক্ষে তার যুক্তি প্রকাশ করেছিলেন। সেটাও…
%22%20transform%3D%22translate(1.6%201.6)%20scale(3.125)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(94.2%2047.2%2083.8)%20scale(29.19333%2062.23519)%22%2F%3E%3Cpath%20d%3D%22M76.8%2055.5l6.4-45.6%20104%2014.6-6.4%2045.6z%22%2F%3E%3Cpath%20fill%3D%22%23262626%22%20d%3D%22M227%2054l44%20103-287-72z%22%2F%3E%3Cellipse%20fill%3D%22%23242424%22%20cx%3D%2246%22%20cy%3D%2232%22%20rx%3D%2235%22%20ry%3D%22255%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
এক চলকবিশিষ্ট বহুপদীর উৎপাদকে বিশ্লেষণ
এক চলক বিশিষ্ট বহুপদী হল বীজগাণিতিক রাশি, যার প্রতিটি পদ C.xⁿ আকারের। যেখানে , n∈ℤ+, আর C হল ধ্রুব। আমার আলোচনায় n≤4 থাকবে আর C পূর্ণসংখ্যা। বহুপদীতে সসীম সংখ্যক পদ থাকবে। একটি পদ থাকলেও বহুপদী হয়। উদাহরণস্বরূপ, 2x³-3 একটি বহুপদী, এর দুটি পদ 2x³ এবং -3 বহুপদীর উৎপাদকে বিশ্লেষণ হল বহুপদীকে একাধিক বহুপদীর গুণফল আকারে…
%27%20fill-opacity%3D%27.5%27%3E%3Cellipse%20fill%3D%22%23252525%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(-151.7%20150.3%20271.8)%20scale(424.61861%20885.46853)%22%2F%3E%3Cellipse%20fill%3D%22%23fff%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(-163%20742%20231.3)%20scale(577.35324%201533.28435)%22%2F%3E%3Cellipse%20fill%3D%22%231d1d1d%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22rotate(20.3%20-2928%20645.6)%20scale(184.81763%20439.71695)%22%2F%3E%3Cellipse%20fill%3D%22%238f8f8f%22%20fill-opacity%3D%22.5%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-1078.7348%20484.86327%20-89.67545%20-199.51197%2047.4%20202.3)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
কথা ছাড়া প্রমাণ: গণিতের সৌন্দর্য
গণিত এক অবাক করা সুন্দরী। এর প্রতিটি বাঁকে রয়েছে অপূর্ব এক মায়া। আজ আমরা গণিতের এক ধরনের প্রমাণের কথা বলব, যার জন্য কোন কথার প্রয়োজন হয় না। শুধু ছবি থেকেই প্রমাণিত হয়ে যায়! সমীকরণের যদি প্রয়োজন হয়ও তবুও তা মাত্র কয়েক লাইন। সবচেয়ে বড় কথা হচ্ছে, এ ধরনের প্রমাণ আমাদের শেখায় কীভাবে গণিতকে অনুভব…
%22%20transform%3D%22translate(.7%20.7)%20scale(1.48438)%22%20fill-opacity%3D%22.5%22%3E%3Cellipse%20fill%3D%22%23d7d46f%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(-20.7014%20122.0238%20-61.71338%20-10.46971%2065%20177.5)%22%2F%3E%3Cellipse%20cx%3D%22215%22%20cy%3D%22230%22%20rx%3D%2287%22%20ry%3D%2287%22%2F%3E%3Cellipse%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(3.53863%20-38.69167%2084.32512%207.71213%20214%2023)%22%2F%3E%3Cellipse%20fill%3D%22%236261e6%22%20rx%3D%221%22%20ry%3D%221%22%20transform%3D%22matrix(41.17405%2030.25818%20-27.588%2037.54059%20211.2%2099.5)%22%2F%3E%3C%2Fg%3E%3C%2Fsvg%3E)
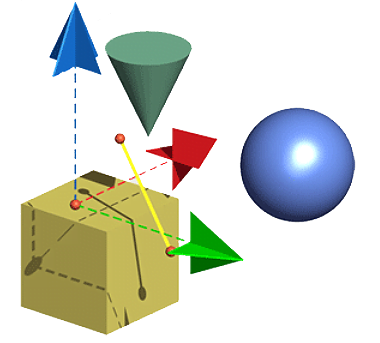
ত্রিমাত্রিক জ্যামিতির কিছু প্রাথমিক আলোচনা
জ্যামিতি গণিতের অত্যন্ত পুরোনো একটি শাখা। খ্রিস্টপূর্ব ২৫০০০ এর আগেও জ্যামিতির ব্যবহার ছিল। প্রথমদিকে জ্যামিতির ব্যবহার ছিল মূলত ভূমি পরিমাপে। কিন্তু আস্তে আস্তে এর বিকাশ ঘটে। প্রথমেই এক্ষেত্রে চলে আসে ইউক্লিডের নাম, যদিও ইউক্লিড একা এই জ্যামিতির প্রণেতা নন, পিথাগোরাস,আর্কিমিদিস, ব্রহ্মগুপ্ত, টলেমি প্রমুখের নামও জড়িয়ে আছে এতে। তবে ইউক্লিডই সর্বপ্রথম The elements এ এসব লিপিবদ্ধ…